Note
Click here to download the full example code
Synthetic seismic¶
This example shows how to use the pylops.utils.seismicevents module
to quickly create synthetic seismic data to be used for toy examples and tests.
import matplotlib.pyplot as plt
import numpy as np
import pylops
plt.close("all")
Let’s first define the time and space axes as well as some auxiliary input parameters that we will use to create a Ricker wavelet
We want to create a 2d data with a number of crossing linear events using the
pylops.utils.seismicevents.linear2d routine.
We can also create a 2d data with a number of crossing parabolic events using the
pylops.utils.seismicevents.parabolic2d routine.
And similarly we can create a 2d data with a number of crossing hyperbolic
events using the pylops.utils.seismicevents.hyperbolic2d routine.
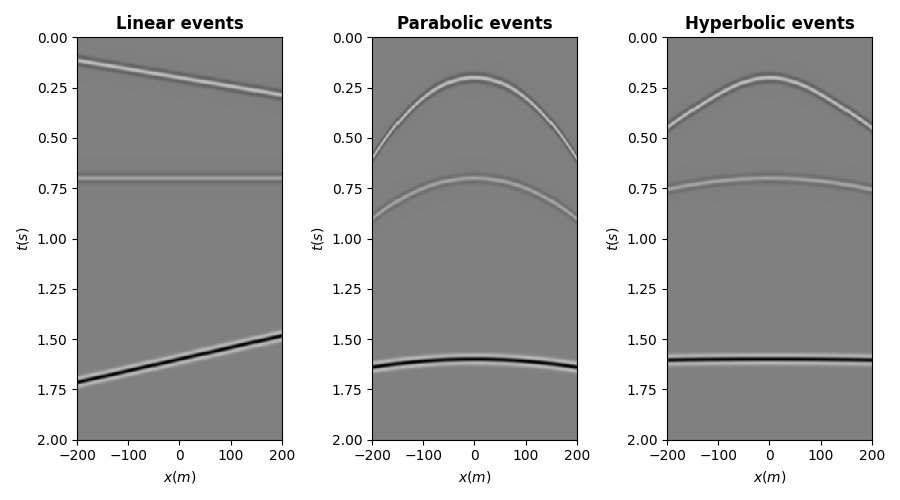
We can now visualize the different events
# sphinx_gallery_thumbnail_number = 2
fig, axs = plt.subplots(1, 3, figsize=(9, 5))
axs[0].imshow(
mlinwav.T,
aspect="auto",
interpolation="nearest",
vmin=-2,
vmax=2,
cmap="gray",
extent=(x.min(), x.max(), t.max(), t.min()),
)
axs[0].set_title("Linear events", fontsize=12, fontweight="bold")
axs[0].set_xlabel(r"$x(m)$")
axs[0].set_ylabel(r"$t(s)$")
axs[1].imshow(
mparwav.T,
aspect="auto",
interpolation="nearest",
vmin=-2,
vmax=2,
cmap="gray",
extent=(x.min(), x.max(), t.max(), t.min()),
)
axs[1].set_title("Parabolic events", fontsize=12, fontweight="bold")
axs[1].set_xlabel(r"$x(m)$")
axs[1].set_ylabel(r"$t(s)$")
axs[2].imshow(
mhypwav.T,
aspect="auto",
interpolation="nearest",
vmin=-2,
vmax=2,
cmap="gray",
extent=(x.min(), x.max(), t.max(), t.min()),
)
axs[2].set_title("Hyperbolic events", fontsize=12, fontweight="bold")
axs[2].set_xlabel(r"$x(m)$")
axs[2].set_ylabel(r"$t(s)$")
plt.tight_layout()
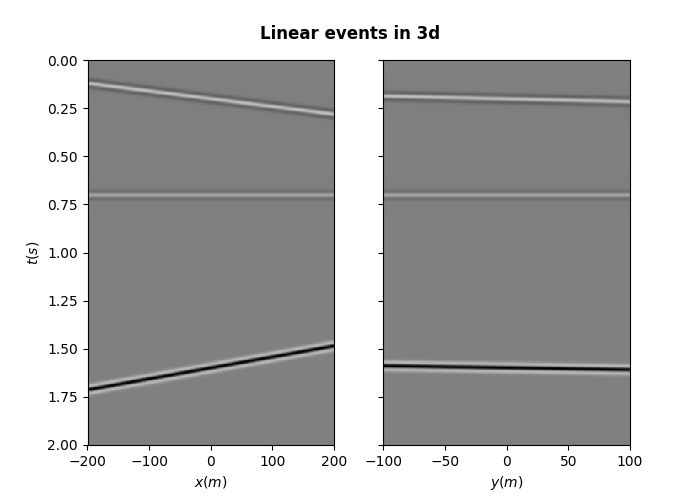
Let’s finally repeat the same exercise in 3d
phi = [20, 0, -10]
mlin, mlinwav = pylops.utils.seismicevents.linear3d(
x, y, t, v, t0, theta, phi, amp, wav
)
fig, axs = plt.subplots(1, 2, figsize=(7, 5), sharey=True)
fig.suptitle("Linear events in 3d", fontsize=12, fontweight="bold", y=0.95)
axs[0].imshow(
mlinwav[par["ny"] // 2].T,
aspect="auto",
interpolation="nearest",
vmin=-2,
vmax=2,
cmap="gray",
extent=(x.min(), x.max(), t.max(), t.min()),
)
axs[0].set_xlabel(r"$x(m)$")
axs[0].set_ylabel(r"$t(s)$")
axs[1].imshow(
mlinwav[:, par["nx"] // 2].T,
aspect="auto",
interpolation="nearest",
vmin=-2,
vmax=2,
cmap="gray",
extent=(y.min(), y.max(), t.max(), t.min()),
)
axs[1].set_xlabel(r"$y(m)$")
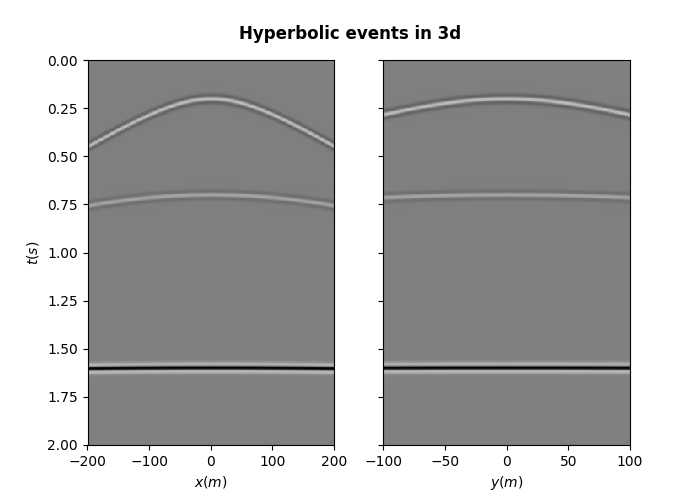
mhyp, mhypwav = pylops.utils.seismicevents.hyperbolic3d(
x, y, t, t0, vrms, vrms, amp, wav
)
fig, axs = plt.subplots(1, 2, figsize=(7, 5), sharey=True)
fig.suptitle("Hyperbolic events in 3d", fontsize=12, fontweight="bold", y=0.95)
axs[0].imshow(
mhypwav[par["ny"] // 2].T,
aspect="auto",
interpolation="nearest",
vmin=-2,
vmax=2,
cmap="gray",
extent=(x.min(), x.max(), t.max(), t.min()),
)
axs[0].set_xlabel(r"$x(m)$")
axs[0].set_ylabel(r"$t(s)$")
axs[1].imshow(
mhypwav[:, par["nx"] // 2].T,
aspect="auto",
interpolation="nearest",
vmin=-2,
vmax=2,
cmap="gray",
extent=(y.min(), y.max(), t.max(), t.min()),
)
axs[1].set_xlabel(r"$y(m)$")
Out:
Text(0.5, 25.722222222222214, '$y(m)$')
Total running time of the script: ( 0 minutes 2.369 seconds)