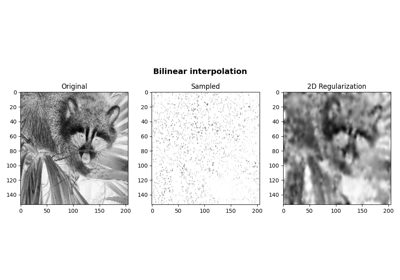
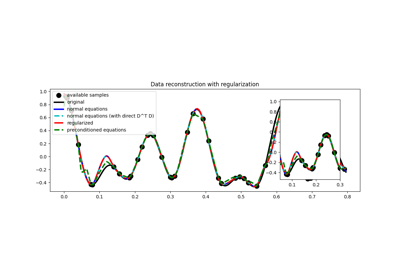
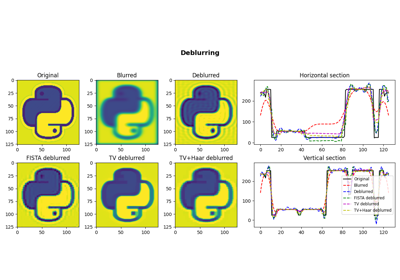
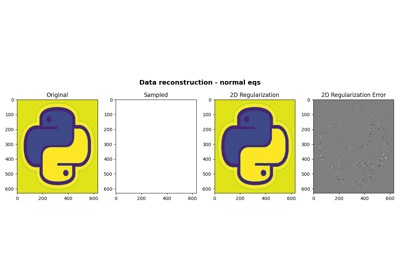
pylops.optimization.leastsquares.NormalEquationsInversion

pylops.optimization.leastsquares.NormalEquationsInversion(Op, Regs, data, Weight=None, dataregs=None, epsI=0, epsRs=None, x0=None, returninfo=False, NRegs=None, epsNRs=None, **kwargs_solver)[source]

Inversion of normal equations.

Solve the regularized normal equations for a system of equations given the operator Op, a data weighting operator Weight and optionally a list of regularization terms Regs and/or NRegs.

Parameters:
Op : pylops.LinearOperator

Operator to invert

Regs : list

Regularization operators (None to avoid adding regularization)

data : numpy.ndarray

Data

Weight : pylops.LinearOperator, optional

Weight operator

dataregs : list, optional

Regularization data (must have the same number of elements as Regs)

epsI : float, optional

Tikhonov damping

epsRs : list, optional

Regularization dampings (must have the same number of elements as Regs)

x0 : numpy.ndarray, optional

Initial guess

returninfo : bool, optional

Return info of CG solver

NRegs : list

Normal regularization operators (None to avoid adding regularization). Such operators must apply the chain of the forward and the adjoint in one go. This can be convenient in cases where a faster implementation is available compared to applying the forward followed by the adjoint.

epsNRs : list, optional

Regularization dampings for normal operators (must have the same number of elements as NRegs)

**kwargs_solver

Arbitrary keyword arguments for chosen solver (scipy.sparse.linalg.cg and pylops.optimization.solver.cg are used as default for numpy and cupy data, respectively)

Note

When user does not supply atol, it is set to “legacy”.
Returns:
xinv : numpy.ndarray

Inverted model.

istop : int

Convergence information:

0: successful exit

>0: convergence to tolerance not achieved, number of iterations

<0: illegal input or breakdown

See also

RegularizedInversion
Regularized inversion
PreconditionedInversion
Preconditioned inversion

Notes

Solve the following normal equations for a system of regularized equations given the operator \(\mathbf{Op}\), a data weighting operator \(\mathbf{W}\), a list of regularization terms (\(\mathbf{R}_i\) and/or \(\mathbf{N}_i\)), the data \(\mathbf{d}\) and regularization data \(\mathbf{d}_{\mathbf{R}_i}\), and the damping factors \(\epsilon_I\), \(\epsilon_{\mathbf{R}_i}\) and \(\epsilon_{\mathbf{N}_i}\):

\[( \mathbf{Op}^T \mathbf{W} \mathbf{Op} + \sum_i \epsilon_{\mathbf{R}_i}^2 \mathbf{R}_i^T \mathbf{R}_i + \sum_i \epsilon_{\mathbf{N}_i}^2 \mathbf{N}_i + \epsilon_I^2 \mathbf{I} ) \mathbf{x} = \mathbf{Op}^T \mathbf{W} \mathbf{d} + \sum_i \epsilon_{\mathbf{R}_i}^2 \mathbf{R}_i^T \mathbf{d}_{\mathbf{R}_i}\]

Note that the data term of the regularizations \(\mathbf{N}_i\) is implicitly assumed to be zero.

Examples using pylops.optimization.leastsquares.NormalEquationsInversion