16. CT Scan Imaging

This tutorial considers a very well-known inverse problem from the field of medical imaging.

We will be using the pylops.signalprocessing.Radon2D operator to model a sinogram, which is a graphic representation of the raw data obtained from a CT scan. The sinogram is further inverted using both a L2 solver and a TV-regularized solver like Split-Bregman.

import matplotlib.pyplot as plt

# sphinx_gallery_thumbnail_number = 2
import numpy as np
from numba import jit

import pylops

plt.close("all")
np.random.seed(10)

Let’s start by loading the Shepp-Logan phantom model. We can then construct the sinogram by providing a custom-made function to the pylops.signalprocessing.Radon2D that samples parametric curves of such a type:

\[t(r,\theta; x) = \tan(90°-\theta)x + \frac{r}{\sin(\theta)}\]

where \(\theta\) is the angle between the x-axis (\(x\)) and the perpendicular to the summation line and \(r\) is the distance from the origin of the summation line.

@jit(nopython=True)
def radoncurve(x, r, theta):
    return (
        (r - ny // 2) / (np.sin(np.deg2rad(theta)) + 1e-15)
        + np.tan(np.deg2rad(90 - theta)) * x
        + ny // 2
    )


x = np.load("../testdata/optimization/shepp_logan_phantom.npy").T
x = x / x.max()
nx, ny = x.shape

ntheta = 150
theta = np.linspace(0.0, 180.0, ntheta, endpoint=False)

RLop = pylops.signalprocessing.Radon2D(
    np.arange(ny),
    np.arange(nx),
    theta,
    kind=radoncurve,
    centeredh=True,
    interp=False,
    engine="numba",
    dtype="float64",
)

y = RLop.H * x.ravel()
y = y.reshape(ntheta, ny)

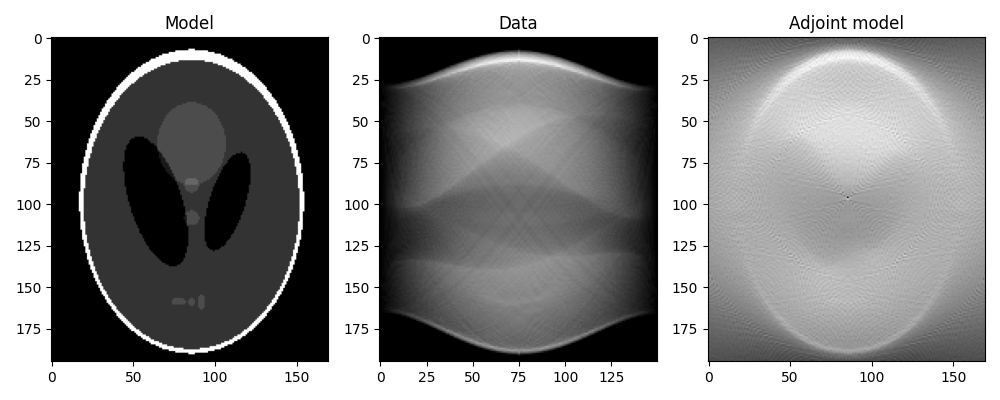
We can now first perform the adjoint, which in the medical imaging literature is also referred to as back-projection.

This is the first step of a common reconstruction technique, named filtered back-projection, which simply applies a correction filter in the frequency domain to the adjoint model.

xrec = RLop * y.ravel()
xrec = xrec.reshape(nx, ny)

fig, axs = plt.subplots(1, 3, figsize=(10, 4))
axs[0].imshow(x.T, vmin=0, vmax=1, cmap="gray")
axs[0].set_title("Model")
axs[0].axis("tight")
axs[1].imshow(y.T, cmap="gray")
axs[1].set_title("Data")
axs[1].axis("tight")
axs[2].imshow(xrec.T, cmap="gray")
axs[2].set_title("Adjoint model")
axs[2].axis("tight")
fig.tight_layout()

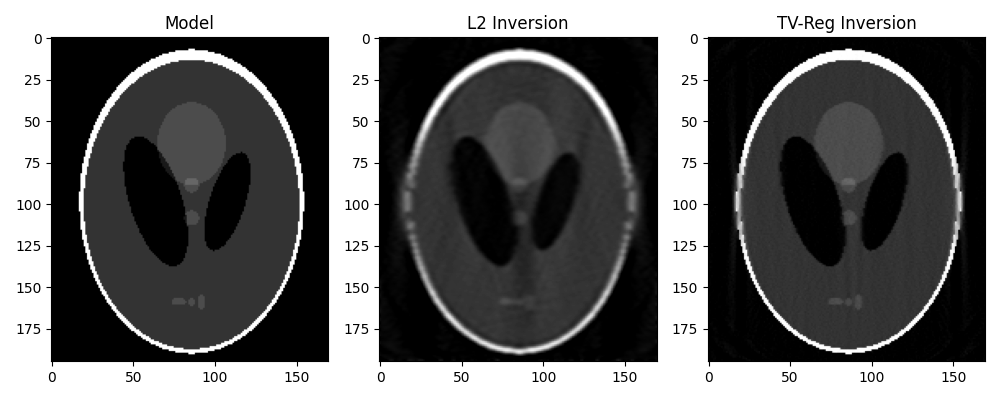
Finally we take advantage of our different solvers and try to invert the modelling operator both in a least-squares sense and using TV-reg.

Dop = [
    pylops.FirstDerivative(
        ny * nx, dims=(nx, ny), dir=0, edge=True, kind="backward", dtype=np.float64
    ),
    pylops.FirstDerivative(
        ny * nx, dims=(nx, ny), dir=1, edge=True, kind="backward", dtype=np.float64
    ),
]
D2op = pylops.Laplacian(dims=(nx, ny), edge=True, dtype=np.float64)

# L2
xinv_sm = pylops.optimization.leastsquares.RegularizedInversion(
    RLop.H, [D2op], y.ravel(), epsRs=[1e1], **dict(iter_lim=20)
)
xinv_sm = np.real(xinv_sm.reshape(nx, ny))

# TV
mu = 1.5
lamda = [1.0, 1.0]
niter = 3
niterinner = 4

xinv, niter = pylops.optimization.sparsity.SplitBregman(
    RLop.H,
    Dop,
    y.ravel(),
    niter,
    niterinner,
    mu=mu,
    epsRL1s=lamda,
    tol=1e-4,
    tau=1.0,
    show=False,
    **dict(iter_lim=20, damp=1e-2)
)
xinv = np.real(xinv.reshape(nx, ny))

fig, axs = plt.subplots(1, 3, figsize=(10, 4))
axs[0].imshow(x.T, vmin=0, vmax=1, cmap="gray")
axs[0].set_title("Model")
axs[0].axis("tight")
axs[1].imshow(xinv_sm.T, vmin=0, vmax=1, cmap="gray")
axs[1].set_title("L2 Inversion")
axs[1].axis("tight")
axs[2].imshow(xinv.T, vmin=0, vmax=1, cmap="gray")
axs[2].set_title("TV-Reg Inversion")
axs[2].axis("tight")
fig.tight_layout()