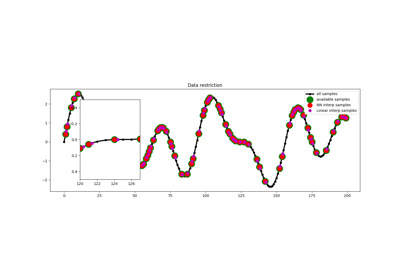
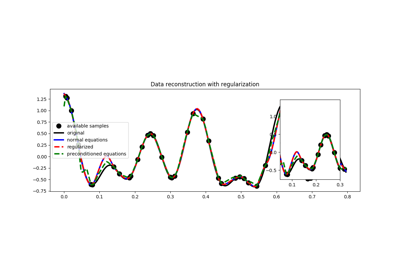
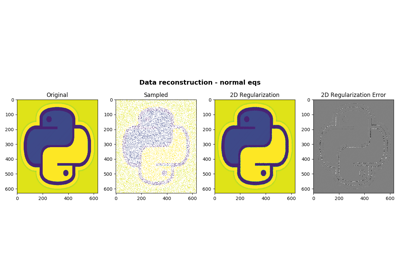
pylops.Restriction¶
-
class
pylops.Restriction(M, iava, dims=None, dir=0, dtype='float64', inplace=True)[source]¶ Restriction (or sampling) operator.
Extract subset of values from input vector at locations
iavain forward mode and place those values at locationsiavain an otherwise zero vector in adjoint mode.Parameters: - M :
int Number of samples in model.
- iava :
listornumpy.ndarray Integer indices of available samples for data selection.
- dims :
list Number of samples for each dimension (
Noneif only one dimension is available)- dir :
int, optional Direction along which restriction is applied.
- dtype :
str, optional Type of elements in input array.
- inplace :
bool, optional Work inplace (
True) or make a new copy (False). By default, data is a reference to the model (in forward) and model is a reference to the data (in adjoint).
See also
pylops.signalprocessing.Interp- Interpolation operator
Notes
Extraction (or sampling) of a subset of \(N\) values at locations
iavafrom an input (or model) vector \(\mathbf{x}\) of size \(M\) can be expressed as:\[y_i = x_{l_i} \quad \forall i=1,2,...,M\]where \(\mathbf{l}=[l_1, l_2,..., l_M]\) is a vector containing the indeces of the original array at which samples are taken.
Conversely, in adjoint mode the available values in the data vector \(\mathbf{y}\) are placed at locations \(\mathbf{l}=[l_1, l_2,..., l_M]\) in the model vector:
\[x_{l_i} = y_i \quad \forall i=1,2,...,M\]and \(x_{j}=0 j \neq l_i\) (i.e., at all other locations in input vector).
Attributes: Methods
__init__(self, M, iava[, dims, dir, dtype, …])Initialize this LinearOperator. adjoint(self)Hermitian adjoint. cond(self, \*\*kwargs_eig)Condition number of linear operator. conj(self)Complex conjugate operator div(self, y[, niter])Solve the linear problem \(\mathbf{y}=\mathbf{A}\mathbf{x}\). dot(self, x)Matrix-matrix or matrix-vector multiplication. eigs(self[, neigs, symmetric, niter])Most significant eigenvalues of linear operator. mask(self, x)Apply mask to input signal returning a signal of same size with values at iavalocations and0at other locationsmatmat(self, X)Matrix-matrix multiplication. matvec(self, x)Matrix-vector multiplication. rmatvec(self, x)Adjoint matrix-vector multiplication. transpose(self)Transpose this linear operator. -
mask(self, x)[source]¶ Apply mask to input signal returning a signal of same size with values at
iavalocations and0at other locationsParameters: - x :
numpy.ndarray Input array (can be either flattened or not)
Returns: - y :
numpy.ma.core.MaskedArray Masked array.
- x :
- M :