pylops.signalprocessing.FFT

pylops.signalprocessing.FFT(dims, dir=0, nfft=None, sampling=1.0, real=False, fftshift=False, engine='numpy', dtype='complex128', **kwargs_fftw)[source]

One dimensional Fast-Fourier Transform.

Apply Fast-Fourier Transform (FFT) along a specific direction dir of a multi-dimensional array of size dim.

Note that the FFT operator is an overload to either the numpy numpy.fft.fft (or numpy.fft.rfft for real models) in forward mode and to the numpy numpy.fft.ifft (or numpy.fft.irfft for real models) in adjoint mode, or to the pyfftw.FFTW class.

In both cases, scaling is properly taken into account to guarantee that the operator is passing the dot-test.

Note

For a real valued input signal, it is possible to store the values of the Fourier transform at positive frequencies only as values at negative frequencies are simply their complex conjugates. However as the operation of removing the negative part of the frequency axis in forward mode and adding the complex conjugates in adjoint mode is nonlinear, the Linear Operator FTT with real=True is not expected to pass the dot-test. It is thus only advised to use this flag when a forward and adjoint FFT is used in the same chained operator (e.g., FFT.H*Op*FFT) such as in pylops.waveeqprocessing.mdd.MDC.

Parameters:
dims : tuple

Number of samples for each dimension

dir : int, optional

Direction along which FFT is applied.

nfft : int, optional

Number of samples in Fourier Transform (same as input if nfft=None)

sampling : float, optional

Sampling step dt.

real : bool, optional

Model to which fft is applied has real numbers (True) or not (False). Used to enforce that the output of adjoint of a real model is real.

fftshift : bool, optional

Apply fftshift/ifftshift (True) or not (False)

engine : str, optional

Engine used for fft computation (numpy or fftw)

dtype : str, optional

Type of elements in input array.

**kwargs_fftw

Arbitrary keyword arguments for pyfftw.FTTW
Raises:
ValueError

If dims is not provided and if dir is bigger than len(dims)

NotImplementedError

If engine is neither numpy nor numba

Notes

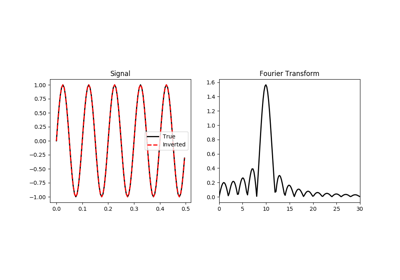
The FFT operator applies the forward Fourier transform to a signal \(d(t)\) in forward mode:

\[D(f) = \mathscr{F} (d) = \int d(t) e^{-j2\pi ft} dt\]

Similarly, the inverse Fourier transform is applied to the Fourier spectrum \(D(f)\) in adjoint mode:

\[d(t) = \mathscr{F}^{-1} (D) = \int D(f) e^{j2\pi ft} df\]

Both operators are effectively discretized and solved by a fast iterative algorithm known as Fast Fourier Transform.

Note that the FFT operator is a special operator in that the adjoint is also the inverse of the forward mode. Moreover, in case of real signal in time domain, the Fourier transform in Hermitian.

Attributes:
shape : tuple

Operator shape

explicit : bool

Operator contains a matrix that can be solved explicitly (True) or not (False)

Examples using pylops.signalprocessing.FFT