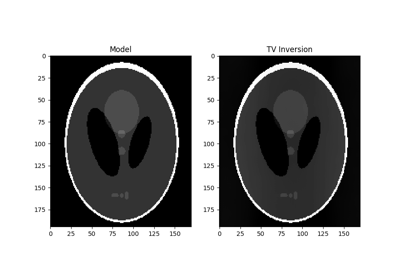
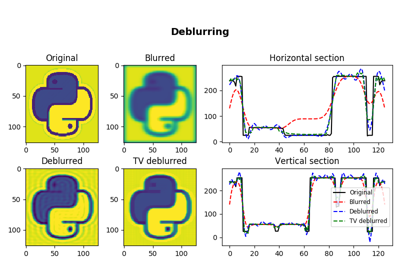
pylops.optimization.sparsity.SplitBregman

pylops.optimization.sparsity.SplitBregman(Op, RegsL1, data, niter_outer=3, niter_inner=5, RegsL2=None, dataregsL2=None, mu=1.0, epsRL1s=None, epsRL2s=None, tol=1e-10, tau=1.0, x0=None, restart=False, show=False, **kwargs_lsqr)

Split Bregman for mixed L2-L1 norms.

Solve an unconstrained system of equations with mixed L2-L1 regularization terms given the operator Op, a list of L1 regularization terms RegsL1, and an optional list of L2 regularization terms RegsL2.

Parameters:

Op : pylops.LinearOperator

Operator to invert

RegsL1 : list

L1 regularization operators

data : numpy.ndarray

Data

niter_outer : int

Number of iterations of outer loop

niter_inner : int

Number of iterations of inner loop

RegsL2 : list

Additional L2 regularization operators (if None, L2 regularization is not added to the problem)

dataregsL2 : list, optional

L2 Regularization data (must have the same number of elements of RegsL2 or equal to None to use a zero data for every regularization operator in RegsL2)

mu : float, optional

Data term damping

epsRL1s : list

L1 Regularization dampings (must have the same number of elements as RegsL1)

epsRL2s : list

L2 Regularization dampings (must have the same number of elements as RegsL2)

tol : float, optional

Tolerance. Stop outer iterations if difference between inverted model at subsequent iterations is smaller than tol

tau : float, optional

Scaling factor in the Bregman update (must be close to 1)

x0 : numpy.ndarray, optional

Initial guess

restart : bool, optional

The unconstrained inverse problem in inner loop is initialized with the initial guess (True) or with the last estimate (False)

show : bool, optional

Display iterations log

**kwargs_lsqr

Arbitrary keyword arguments for scipy.sparse.linalg.lsqr solver

Returns:

xinv : numpy.ndarray

Inverted model

itn_out : int

Iteration number of outer loop upon termination

Notes

Solve the following system of unconstrained, regularized equations given the operator \(\mathbf{Op}\) and a set of mixed norm (L2 and L1) regularization terms \(\mathbf{R_{L2,i}}\) and \(\mathbf{R_{L1,i}}\), respectively:

\[J = \mu/2 ||\textbf{d} - \textbf{Op} \textbf{x} |||_2 + \sum_i \epsilon_{{R}_{L2,i}} ||\mathbf{d_{{R}_{L2,i}}} - \mathbf{R_{L2,i}} \textbf{x} |||_2 + \sum_i || \mathbf{R_{L1,i}} \textbf{x} |||_1\]

where \(\mu\) and \(\epsilon_{{R}_{L2,i}}\) are the damping factors used to weight the different terms of the cost function.

The generalized Split Bergman algorithm is used to solve such cost function: the algorithm is composed of a sequence of unconstrained inverse problems and Bregman updates. Note that the L1 terms are not weighted in the original cost function but are first converted into constraints and then re-inserted in the cost function with Lagrange multipliers \(\epsilon_{{R}_{L1,i}}\), which effectively act as damping factors for those terms. See [1] for detailed derivation.

The scipy.sparse.linalg.lsqr solver and a fast shrinkage algorithm are used within the inner loop to solve the unconstrained inverse problem, and the same procedure is repeated niter_outer times until convergence.

[1]	Goldstein T. and Osher S., “The Split Bregman Method for L1-Regularized Problems”, SIAM J. on Scientific Computing, vol. 2(2), pp. 323-343. 2008.

Examples using pylops.optimization.sparsity.SplitBregman

Total Variation (TV) Regularization

04. Image deblurring