pylops.Sum

class pylops.Sum(dims, dir, dtype='float64')

Sum operator.

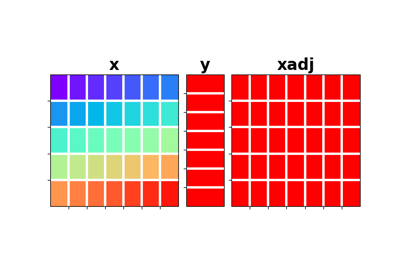
Sum along an axis of a multi-dimensional array (at least 2 dimensions are required) in forward model, and spread along the same axis in adjoint mode.

Parameters:

dims : tuple

Number of samples for each dimension

dir : int

Direction along which summation is performed.

dtype : str, optional

Type of elements in input array.

Notes

Given a two dimensional array, the Sum operator re-arranges the input model into a multi-dimensional array of size dims and sums values along direction dir:

\[y_j = \sum_i x_{i, j}\]

In adjoint mode, the data is spread along the same direction:

\[x_{i, j} = y_j \quad \forall i=0, N-1\]

Attributes:

shape : tuple

Operator shape

explicit : bool

Operator contains a matrix that can be solved explicitly (True) or not (False)

Methods

__init__(dims, dir[, dtype])	Initialize this LinearOperator.
adjoint()	Hermitian adjoint.
apply_columns(cols)	Apply subset of columns of operator
cond([uselobpcg])	Condition number of linear operator.
conj()	Complex conjugate operator
div(y[, niter, densesolver])	Solve the linear problem \(\mathbf{y}=\mathbf{A}\mathbf{x}\).
dot(x)	Matrix-matrix or matrix-vector multiplication.
eigs([neigs, symmetric, niter, uselobpcg])	Most significant eigenvalues of linear operator.
matmat(X)	Matrix-matrix multiplication.
matvec(x)	Matrix-vector multiplication.
rmatmat(X)	Matrix-matrix multiplication.
rmatvec(x)	Adjoint matrix-vector multiplication.
todense([backend])	Return dense matrix.
toimag([forw, adj])	Imag operator
toreal([forw, adj])	Real operator
tosparse()	Return sparse matrix.
trace([neval, method, backend])	Trace of linear operator.
transpose()	Transpose this linear operator.

Examples using pylops.Sum

Sum