pylops.Transpose

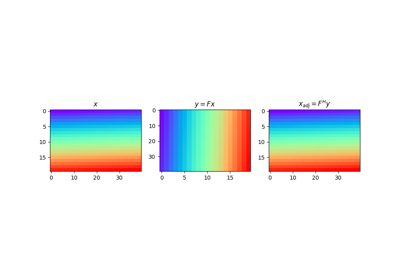
class pylops.Transpose(dims, axes, dtype='float64')

Transpose operator.

Transpose axes of a multi-dimensional array. This operator works with flattened input model (or data), which are however multi-dimensional in nature and will be reshaped and treated as such in both forward and adjoint modes.

Parameters:

dims : tuple, optional

Number of samples for each dimension

axes : tuple, optional

Direction along which transposition is applied

dtype : str, optional

Type of elements in input array

Raises:

ValueError

If axes contains repeated dimensions (or a dimension is missing)

Notes

The Transpose operator reshapes the input model into a multi-dimensional array of size dims and transposes (or swaps) its axes as defined in axes.

Similarly, in adjoint mode the data is reshaped into a multi-dimensional array whose size is a permuted version of dims defined by axes. The array is then rearragned into the original model dimensions dims.

Attributes:

shape : tuple

Operator shape

explicit : bool

Operator contains a matrix that can be solved explicitly (True) or not (False)

Methods

__init__(dims, axes[, dtype])	Initialize this LinearOperator.
adjoint()	Hermitian adjoint.
apply_columns(cols)	Apply subset of columns of operator
cond([uselobpcg])	Condition number of linear operator.
conj()	Complex conjugate operator
div(y[, niter, densesolver])	Solve the linear problem \(\mathbf{y}=\mathbf{A}\mathbf{x}\).
dot(x)	Matrix-matrix or matrix-vector multiplication.
eigs([neigs, symmetric, niter, uselobpcg])	Most significant eigenvalues of linear operator.
matmat(X)	Matrix-matrix multiplication.
matvec(x)	Matrix-vector multiplication.
rmatmat(X)	Matrix-matrix multiplication.
rmatvec(x)	Adjoint matrix-vector multiplication.
todense([backend])	Return dense matrix.
toimag([forw, adj])	Imag operator
toreal([forw, adj])	Real operator
tosparse()	Return sparse matrix.
trace([neval, method, backend])	Trace of linear operator.
transpose()	Transpose this linear operator.

Examples using pylops.Transpose

Transpose