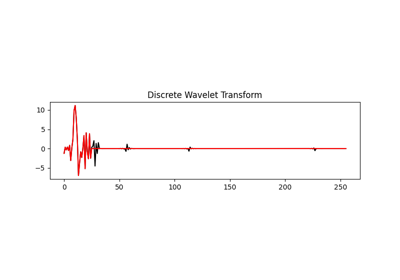
pylops.signalprocessing.DWT¶
-
class
pylops.signalprocessing.DWT(dims, dir=0, wavelet='haar', level=1, dtype='float64')[source]¶ One dimensional Wavelet operator.
Apply 1D-Wavelet Transform along a specific direction
dirof a multi-dimensional array of sizedims.Note that the Wavelet operator is an overload of the
pywtimplementation of the wavelet transform. Refer to https://pywavelets.readthedocs.io for a detailed description of the input parameters.Parameters: - dims :
intortuple Number of samples for each dimension
- dir :
int, optional Direction along which DWT is applied.
- wavelet :
str, optional Name of wavelet type. Use
pywt.wavelist(kind='discrete')for a list of available wavelets.- level :
int, optional Number of scaling levels (must be >=0).
- dtype :
str, optional Type of elements in input array.
Raises: - ModuleNotFoundError
If
pywtis not installed- ValueError
If
waveletdoes not belong topywt.families
Notes
The Wavelet operator applies the multilevel Discrete Wavelet Transform (DWT) in forward mode and the multilevel Inverse Discrete Wavelet Transform (IDWT) in adjoint mode.
Wavelet transforms can be used to compress signals and present a key advantage over Fourier transforms in that they captures both frequency and location information in time. Consider using this operator as sparsifying transform when using L1 solvers.
Attributes: Methods
__init__(dims[, dir, wavelet, level, dtype])Initialize this LinearOperator. adjoint()Hermitian adjoint. apply_columns(cols)Apply subset of columns of operator cond([uselobpcg])Condition number of linear operator. conj()Complex conjugate operator div(y[, niter, densesolver])Solve the linear problem \(\mathbf{y}=\mathbf{A}\mathbf{x}\). dot(x)Matrix-matrix or matrix-vector multiplication. eigs([neigs, symmetric, niter, uselobpcg])Most significant eigenvalues of linear operator. matmat(X)Matrix-matrix multiplication. matvec(x)Matrix-vector multiplication. rmatmat(X)Matrix-matrix multiplication. rmatvec(x)Adjoint matrix-vector multiplication. todense([backend])Return dense matrix. toimag([forw, adj])Imag operator toreal([forw, adj])Real operator tosparse()Return sparse matrix. trace([neval, method, backend])Trace of linear operator. transpose()Transpose this linear operator. - dims :