pylops.signalprocessing.Shift

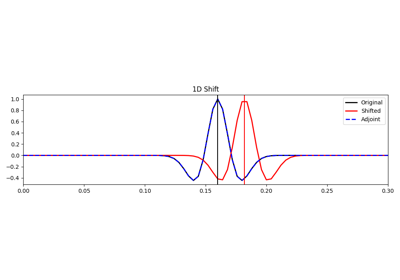
pylops.signalprocessing.Shift(dims, shift, dir=0, nfft=None, sampling=1.0, real=False, engine='numpy', dtype='complex128', **kwargs_fftw)[source]

Shift operator

Apply fractional shift in the frequency domain along a specific direction dir of a multi-dimensional array of size dim.

Parameters:
dims : tuple

Number of samples for each dimension

shift : float

Fractional shift to apply in the same unit as sampling.

dir : int, optional

Direction along which FFT is applied.

nfft : int, optional

Number of samples in Fourier Transform (same as input if nfft=None)

sampling : float, optional

Sampling step \(\Delta t\).

real : bool, optional

Model to which fft is applied has real numbers (True) or not (False). Used to enforce that the output of adjoint of a real model is real.

engine : str, optional

Engine used for fft computation (numpy, scipy, or fftw). Choose numpy when working with CuPy arrays.

dtype : str, optional

Type of elements in input array.

**kwargs_fftw

Arbitrary keyword arguments for pyfftw.FTTW
Raises:
ValueError

If dims is provided and dir is bigger than len(dims)

NotImplementedError

If engine is neither numpy, scipy, nor fftw

Notes

The Shift operator applies the forward Fourier transform, an element-wise complex scaling, and inverse fourier transform

\[\mathbf{y}= \mathbf{F}^{-1} \mathbf{S} \mathbf{F} \mathbf{x}\]

Here \(\mathbf{S}\) is a diagonal operator that scales the Fourier transformed input by \(e^{-j2\pi f t_S}\), where \(t_S\) is the chosen shift.

Attributes:
shape : tuple

Operator shape

explicit : bool

Operator contains a matrix that can be solved explicitly (True) or not (False)

Examples using pylops.signalprocessing.Shift