pylops.waveeqprocessing.Deghosting¶
-
pylops.waveeqprocessing.Deghosting(p, nt, nr, dt, dr, vel, zrec, pd=None, win=None, npad=(11, 11), ntaper=(11, 11), restriction=None, sptransf=None, solver=<function lsqr>, dottest=False, dtype='complex128', **kwargs_solver)[source]¶ Wavefield deghosting.
Apply seismic wavefield decomposition from single-component (pressure) data. This process is also generally referred to as model-based deghosting.
Parameters: - p :
np.ndarray Pressure data of of size \(\lbrack n_{r_x}\,(\times n_{r_y}) \times n_t \rbrack\) (or \(\lbrack n_{r_{x,\text{sub}}}\, (\times n_{r_{y,\text{sub}}}) \times n_t \rbrack\) in case a
restrictionoperator is provided. Note that \(n_{r_{x,\text{sub}}}\) (and \(n_{r_{y,\text{sub}}}\)) must agree with the size of the output of this operator)- nt :
int Number of samples along the time axis
- nr :
intortuple Number of samples along the receiver axis (or axes)
- dt :
float Sampling along the time axis
- dr :
floatortuple Sampling along the receiver array of the separated pressure consituents
- vel :
float Velocity along the receiver array (must be constant)
- zrec :
float Depth of receiver array
- pd :
np.ndarray, optional Direct arrival to be subtracted from
p- win :
np.ndarray, optional Time window to be applied to
pto remove the direct arrival (ifpd=None)- ntaper :
floatortuple, optional Number of samples of taper applied to propagator to avoid edge effects
- npad :
floatortuple, optional Number of samples of padding applied to propagator to avoid edge effects
- restriction :
pylops.LinearOperator, optional Restriction operator
- sptransf :
pylops.LinearOperator, optional Sparsifying operator
- solver :
float, optional Function handle of solver to be used if
kind='inverse'- dottest :
bool, optional Apply dot-test
- dtype :
str, optional Type of elements in input array. If
None, directly inferred fromp- **kwargs_solver
Arbitrary keyword arguments for chosen
solver
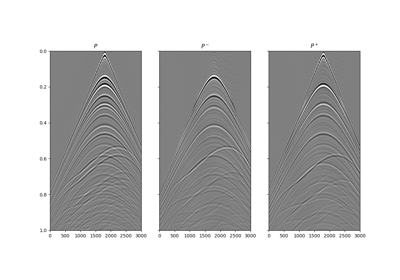
Returns: - pup :
np.ndarray Up-going wavefield
- pdown :
np.ndarray Down-going wavefield
Notes
Up- and down-going components of seismic data \(p^-(x, t)\) and \(p^+(x, t)\) can be estimated from single-component data \(p(x, t)\) using a ghost model.
The basic idea [1] is that of using a one-way propagator in the f-k domain (also referred to as ghost model) to predict the down-going field from the up-going one (excluded the direct arrival and its source ghost referred here to as \(p_d(x, t)\)):
\[p^+ - p_d = e^{-j k_z 2 z_\text{rec}} p^-\]where \(k_z\) is the vertical wavenumber and \(z_\text{rec}\) is the depth of the array of receivers
In a matrix form we can thus write the total wavefield as:
\[\mathbf{p} - \mathbf{p_d} = (\mathbf{I} + \Phi) \mathbf{p}^-\]where \(\Phi\) is one-way propagator implemented via the
pylops.waveeqprocessing.PhaseShiftoperator.[1] Amundsen, L., 1993, Wavenumber-based filtering of marine point-source data: GEOPHYSICS, 58, 1335–1348. - p :