pylops.LinearOperator¶
-
class
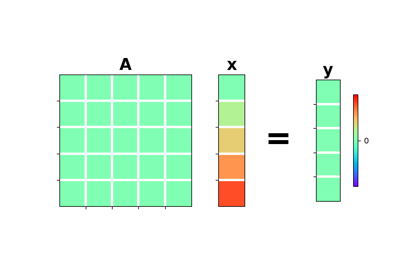
pylops.LinearOperator(Op=None, explicit=False, clinear=None)[source]¶ Common interface for performing matrix-vector products.
This class is an overload of the
scipy.sparse.linalg.LinearOperatorclass. It adds functionalities by overloading standard operators such as__truediv__as well as creating convenience methods such aseigs,cond, andconj.Note
End users of PyLops should not use this class directly but simply use operators that are already implemented. This class is meant for developers and it has to be used as the parent class of any new operator developed within PyLops. Find more details regarding implementation of new operators at Implementing new operators.
Parameters: - Op :
scipy.sparse.linalg.LinearOperatororscipy.sparse.linalg._ProductLinearOperatororscipy.sparse.linalg._SumLinearOperator Operator
- explicit :
bool Operator contains a matrix that can be solved explicitly (
True) or not (False)- clinear :
bool New in version 1.17.0.
Operator is complex-linear.
Methods
__init__([Op, explicit, clinear])Initialize this LinearOperator. adjoint()Hermitian adjoint. apply_columns(cols)Apply subset of columns of operator cond([uselobpcg])Condition number of linear operator. conj()Complex conjugate operator div(y[, niter, densesolver])Solve the linear problem \(\mathbf{y}=\mathbf{A}\mathbf{x}\). dot(x)Matrix-matrix or matrix-vector multiplication. eigs([neigs, symmetric, niter, uselobpcg])Most significant eigenvalues of linear operator. matmat(X)Matrix-matrix multiplication. matvec(x)Matrix-vector multiplication. rmatmat(X)Matrix-matrix multiplication. rmatvec(x)Adjoint matrix-vector multiplication. todense([backend])Return dense matrix. toimag([forw, adj])Imag operator toreal([forw, adj])Real operator tosparse()Return sparse matrix. trace([neval, method, backend])Trace of linear operator. transpose()Transpose this linear operator. -
matvec(x)[source]¶ Matrix-vector multiplication.
Modified version of scipy matvec which does not consider the case where the input vector is
np.matrix(the usenp.matrixis now discouraged in numpy’s documentation).Parameters: - x :
numpy.ndarray Input array of shape (N,) or (N,1)
Returns: - y :
numpy.ndarray Output array of shape (M,) or (M,1)
- x :
-
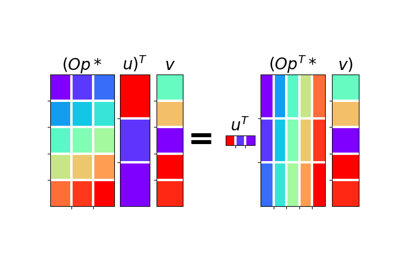
rmatvec(x)[source]¶ Adjoint matrix-vector multiplication.
Modified version of scipy rmatvec which does not consider the case where the input vector is
np.matrix(the usenp.matrixis now discouraged in numpy’s documentation).Parameters: - y :
numpy.ndarray Input array of shape (M,) or (M,1)
Returns: - x :
numpy.ndarray Output array of shape (N,) or (N,1)
- y :
-
matmat(X)[source]¶ Matrix-matrix multiplication.
Modified version of scipy matmat which does not consider the case where the input vector is
np.matrix(the usenp.matrixis now discouraged in numpy’s documentation).Parameters: - x :
numpy.ndarray Input array of shape (N,K)
Returns: - y :
numpy.ndarray Output array of shape (M,K)
- x :
-
rmatmat(X)[source]¶ Matrix-matrix multiplication.
Modified version of scipy rmatmat which does not consider the case where the input vector is
np.matrix(the usenp.matrixis now discouraged in numpy’s documentation).Parameters: - x :
numpy.ndarray Input array of shape (M,K)
Returns: - y :
numpy.ndarray Output array of shape (N,K)
- x :
-
dot(x)[source]¶ Matrix-matrix or matrix-vector multiplication.
Parameters: - x : np.ndarray
Input array (or matrix)
Returns: - y : np.ndarray
Output array (or matrix) that represents the result of applying the linear operator on x.
-
div(y, niter=100, densesolver='scipy')[source]¶ Solve the linear problem \(\mathbf{y}=\mathbf{A}\mathbf{x}\).
Overloading of operator
/to improve expressivity of Pylops when solving inverse problems.Parameters: Returns: - xest :
np.ndarray Estimated model
- xest :
-
todense(backend='numpy')[source]¶ Return dense matrix.
The operator is converted into its dense matrix equivalent. In order to do so, square or tall operators are applied to an identity matrix whose number of rows and columns is equivalent to the number of columns of the operator. Conversely, for skinny operators, the transpose operator is applied to an identity matrix whose number of rows and columns is equivalent to the number of rows of the operator and the resulting matrix is transposed (and complex conjugated).
Note that this operation may be costly for operators with large number of rows and columns and it should be used mostly as a way to inspect the structure of the matricial equivalent of the operator.
Parameters: - backend :
str, optional Backend used to densify matrix (
numpyorcupy). Note that this must be consistent with how the operator has been created.
Returns: - matrix :
numpy.ndarrayorcupy.ndarray Dense matrix.
- backend :
-
tosparse()[source]¶ Return sparse matrix.
The operator in converted into its sparse (CSR) matrix equivalent. In order to do so, the operator is applied to series of unit vectors with length equal to the number of coloumns in the original operator.
Returns: - matrix :
scipy.sparse.csr_matrix Sparse matrix.
- matrix :
-
eigs(neigs=None, symmetric=False, niter=None, uselobpcg=False, **kwargs_eig)[source]¶ Most significant eigenvalues of linear operator.
Return an estimate of the most significant eigenvalues of the linear operator. If the operator has rectangular shape (
shape[0]!=shape[1]), eigenvalues are first computed for the square operator \(\mathbf{A^H}\mathbf{A}\) and the square-root values are returned.Parameters: - neigs :
int Number of eigenvalues to compute (if
None, return all). Note that forexplicit=False, only \(N-1\) eigenvalues can be computed where \(N\) is the size of the operator in the model space- symmetric :
bool, optional Operator is symmetric (
True) or not (False). User should set this parameter toTrueonly when it is guaranteed that the operator is real-symmetric or complex-hermitian matrices- niter :
int, optional Number of iterations for eigenvalue estimation
- uselobpcg :
bool, optional - **kwargs_eig
Arbitrary keyword arguments for
scipy.sparse.linalg.eigs,scipy.sparse.linalg.eigsh, orscipy.sparse.linalg.lobpcg
Returns: - eigenvalues :
numpy.ndarray Operator eigenvalues.
Raises: - ValueError
If
uselobpcg=Truefor a non-symmetric square matrix with complex type
Notes
Depending on the size of the operator, whether it is explicit or not and the number of eigenvalues requested, different algorithms are used by this routine.
More precisely, when only a limited number of eigenvalues is requested the
scipy.sparse.linalg.eigshmethod is used in case ofsymmetric=Trueand thescipy.sparse.linalg.eigsmethod is usedsymmetric=False. However, when the matrix is represented explicitly within the linear operator (explicit=True) and all the eigenvalues are requested thescipy.linalg.eigvalsis used instead.Finally, when only a limited number of eigenvalues is required, it is also possible to explicitly choose to use the
scipy.sparse.linalg.lobpcgmethod via theuselobpcginput parameter flag.Most of these algorithms are a port of ARPACK [1], a Fortran package which provides routines for quickly finding eigenvalues/eigenvectors of a matrix. As ARPACK requires only left-multiplication by the matrix in question, eigenvalues/eigenvectors can also be estimated for linear operators when the dense matrix is not available.
[1] http://www.caam.rice.edu/software/ARPACK/ - neigs :
-
cond(uselobpcg=False, **kwargs_eig)[source]¶ Condition number of linear operator.
Return an estimate of the condition number of the linear operator as the ratio of the largest and lowest estimated eigenvalues.
Parameters: - uselobpcg :
bool, optional Use
scipy.sparse.linalg.lobpcgto compute eigenvalues- **kwargs_eig
Arbitrary keyword arguments for
scipy.sparse.linalg.eigs,scipy.sparse.linalg.eigsh, orscipy.sparse.linalg.lobpcg
Returns: - eigenvalues :
numpy.ndarray Operator eigenvalues.
Notes
The condition number of a matrix (or linear operator) can be estimated as the ratio of the largest and lowest estimated eigenvalues:
\[k= \frac{\lambda_{max}}{\lambda_{min}}\]The condition number provides an indication of the rate at which the solution of the inversion of the linear operator \(A\) will change with respect to a change in the data \(y\).
Thus, if the condition number is large, even a small error in \(y\) may cause a large error in \(x\). On the other hand, if the condition number is small then the error in \(x\) is not much bigger than the error in \(y\). A problem with a low condition number is said to be well-conditioned, while a problem with a high condition number is said to be ill-conditioned.
- uselobpcg :
-
conj()[source]¶ Complex conjugate operator
Returns: - conjop :
pylops.LinearOperator Complex conjugate operator
- conjop :
-
apply_columns(cols)[source]¶ Apply subset of columns of operator
This method can be used to wrap a LinearOperator and mimic the action of a subset of columns of the operator on a reduced model in forward mode, and retrieve only the result of a subset of rows in adjoint mode.
Note that unless the operator has
explicit=True, this is not optimal as the entire forward and adjoint passes of the original operator will have to be perfomed. It can however be useful for the implementation of solvers such as Orthogonal Matching Pursuit (OMP) that iteratively build a solution by evaluate only a subset of the columns of the operator.Parameters: - cols :
list Columns to be selected
Returns: - colop :
pylops.LinearOperator Apply column operator
- cols :
-
toreal(forw=True, adj=True)[source]¶ Real operator
Parameters: Returns: - realop :
pylops.LinearOperator Real operator
- realop :
-
toimag(forw=True, adj=True)[source]¶ Imag operator
Parameters: Returns: - imagop :
pylops.LinearOperator Imag operator
- imagop :
-
trace(neval=None, method=None, backend='numpy', **kwargs_trace)[source]¶ Trace of linear operator.
Returns the trace (or its estimate) of the linear operator.
Parameters: - neval :
int, optional Maximum number of matrix-vector products compute. Default depends
method.- method :
str, optional Should be one of the following:
- explicit: If the operator is not explicit, will convert to dense first.
- hutchinson: see
pylops.utils.trace_hutchinson - hutch++: see
pylops.utils.trace_hutchpp - na-hutch++: see
pylops.utils.trace_nahutchpp
Defaults to ‘explicit’ for explicit operators, and ‘Hutch++’ for the rest.
- backend :
str, optional Backend used to densify matrix (
numpyorcupy). Note that this must be consistent with how the operator has been created.- **kwargs_trace
Arbitrary keyword arguments passed to
pylops.utils.trace_hutchinson,pylops.utils.trace_hutchpp, orpylops.utils.trace_nahutchpp
Returns: - trace :
self.dtype Operator trace.
Raises: - ValueError
If the operator has rectangular shape (
shape[0] != shape[1])- NotImplementedError
If the
methodis not one of the available methods.
- neval :
- Op :