2D Patching

This example shows how to use the pylops.signalprocessing.Patch2D operator to perform repeated transforms over small patches of a 2-dimensional array. The transform that we apply in this example is the pylops.signalprocessing.FFT2D but this operator has been design to allow a variety of transforms as long as they operate with signals that are 2-dimensional in nature, respectively.

import matplotlib.pyplot as plt
import numpy as np

import pylops

plt.close("all")

Let’s start by creating an 2-dimensional array of size \(n_x \times n_t\) composed of 3 parabolic events

par = {"ox": -140, "dx": 2, "nx": 140, "ot": 0, "dt": 0.004, "nt": 200, "f0": 20}

v = 1500
t0 = [0.2, 0.4, 0.5]
px = [0, 0, 0]
pxx = [1e-5, 5e-6, 1e-20]
amp = [1.0, -2, 0.5]

# Create axis
t, t2, x, y = pylops.utils.seismicevents.makeaxis(par)

# Create wavelet
wav = pylops.utils.wavelets.ricker(t[:41], f0=par["f0"])[0]

# Generate model
_, data = pylops.utils.seismicevents.parabolic2d(x, t, t0, px, pxx, amp, wav)

We want to divide this 2-dimensional data into small overlapping patches in the spatial direction and apply the adjoint of the pylops.signalprocessing.FFT2D operator to each patch. This is done by simply using the adjoint of the pylops.signalprocessing.Patch2D operator. Note that for non- orthogonal operators, this must be replaced by an inverse.

nwins = (13, 6)
nwin = (20, 34)
nop = (128, 128)
nover = (10, 4)

dimsd = data.shape
dims = (nwins[0] * nop[0], nwins[1] * nop[1])


# Sliding window transform without taper
Op = pylops.signalprocessing.FFT2D(nwin, nffts=nop)
Slid = pylops.signalprocessing.Patch2D(
    Op.H, dims, dimsd, nwin, nover, nop, tapertype=None, design=False
)
fftdata = Slid.H * data.ravel()

We now create a similar operator but we also add a taper to the overlapping parts of the patches. We then apply the forward to restore the original signal.

Slid = pylops.signalprocessing.Patch2D(
    Op.H, dims, dimsd, nwin, nover, nop, tapertype="hanning", design=False
)

reconstructed_data = Slid * fftdata.ravel()
reconstructed_data = np.real(reconstructed_data.reshape(dimsd))

Finally we re-arrange the transformed patches so that we can also display them

fftdatareshaped = np.zeros((nop[0] * nwins[0], nop[1] * nwins[1]), dtype=fftdata.dtype)

iwin = 1
for ix in range(nwins[0]):
    for it in range(nwins[1]):
        fftdatareshaped[
            ix * nop[0] : (ix + 1) * nop[0], it * nop[1] : (it + 1) * nop[1]
        ] = np.fft.fftshift(
            fftdata[nop[0] * nop[1] * (iwin - 1) : nop[0] * nop[1] * iwin].reshape(nop)
        )
        iwin += 1

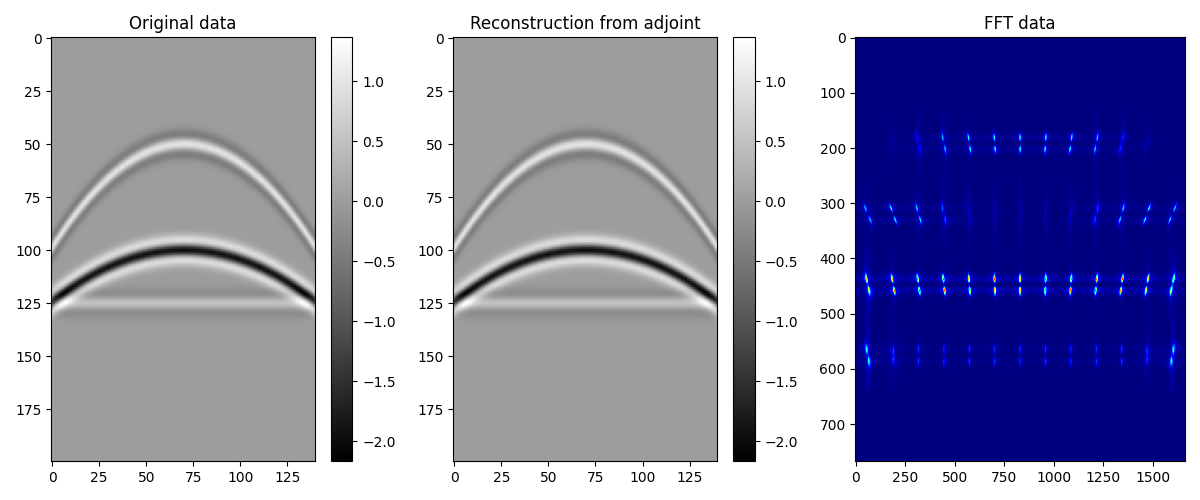
Let’s finally visualize all the intermediate results as well as our final data reconstruction after inverting the pylops.signalprocessing.Sliding2D operator.

fig, axs = plt.subplots(1, 3, figsize=(12, 5))
im = axs[0].imshow(data.T, cmap="gray")
axs[0].set_title("Original data")
plt.colorbar(im, ax=axs[0])
axs[0].axis("tight")
im = axs[1].imshow(reconstructed_data.T, cmap="gray")
axs[1].set_title("Reconstruction from adjoint")
plt.colorbar(im, ax=axs[1])
axs[1].axis("tight")
axs[2].imshow(np.abs(fftdatareshaped).T, cmap="jet")
axs[2].set_title("FFT data")
axs[2].axis("tight")
plt.tight_layout()