01. The LinearOperator

This first tutorial is aimed at easing the use of the PyLops library for both new users and developers.

We will start by looking at how to initialize a linear operator as well as different ways to apply the forward and adjoint operations. We will then investigate various special methods, also called magic methods (i.e., methods with the double underscores at the beginning and the end) that have been implemented for such a class and will allow summing, subtracting, chaining, etc. multiple operators in very easy and expressive way.

Finally, we will consider a scenario where the input and output vectors of an operator are naturally represented by nd-arrays. Since pylops V2, we can both pass to the operator a flattened array (original behaviour) as well as the nd-array with shape dims (new behaviour); according to input, the output will be either a vector or a nd-array with shape dimsd.

Let’s start by defining a simple operator that applies element-wise multiplication of the model with a vector d in forward mode and element-wise multiplication of the data with the same vector d in adjoint mode. This operator is present in PyLops under the name of pylops.Diagonal and its implementation is discussed in more details in the Implementing new operators page.

import timeit

import matplotlib.pyplot as plt
import numpy as np

import pylops

n = 10
d = np.arange(n) + 1.0
x = np.ones(n)
Dop = pylops.Diagonal(d)

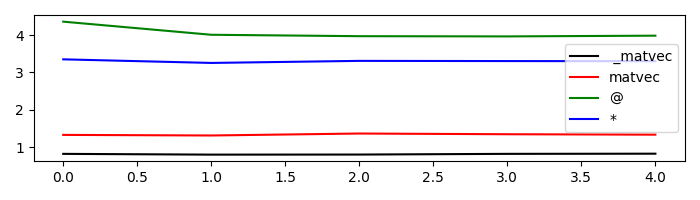
First of all we apply the operator in the forward mode. This can be done in four different ways:

• _matvec: directly applies the method implemented for forward mode

• matvec: performs some checks before and after applying _matvec

• *: operator used to map the special method __matmul__ which checks whether the input x is a vector or matrix and applies _matvec or _matmul accordingly.

• @: operator used to map the special method __mul__ which performs like the * operator

We will time these 4 different executions and see how using _matvec (or matvec) will result in the faster computation. It is thus advised to use * (or @) in examples when expressivity has priority but prefer _matvec (or matvec) for efficient implementations.

# setup command
cmd_setup = """\
import numpy as np
import pylops
n = 10
d = np.arange(n) + 1.
x = np.ones(n)
Dop = pylops.Diagonal(d)
DopH = Dop.H
"""

# _matvec
cmd1 = "Dop._matvec(x)"

# matvec
cmd2 = "Dop.matvec(x)"

# @
cmd3 = "Dop@x"

# *
cmd4 = "Dop*x"

# timing
t1 = 1.0e3 * np.array(timeit.repeat(cmd1, setup=cmd_setup, number=500, repeat=5))
t2 = 1.0e3 * np.array(timeit.repeat(cmd2, setup=cmd_setup, number=500, repeat=5))
t3 = 1.0e3 * np.array(timeit.repeat(cmd3, setup=cmd_setup, number=500, repeat=5))
t4 = 1.0e3 * np.array(timeit.repeat(cmd4, setup=cmd_setup, number=500, repeat=5))

plt.figure(figsize=(7, 2))
plt.plot(t1, "k", label=" _matvec")
plt.plot(t2, "r", label="matvec")
plt.plot(t3, "g", label="@")
plt.plot(t4, "b", label="*")
plt.axis("tight")
plt.legend()
plt.tight_layout()

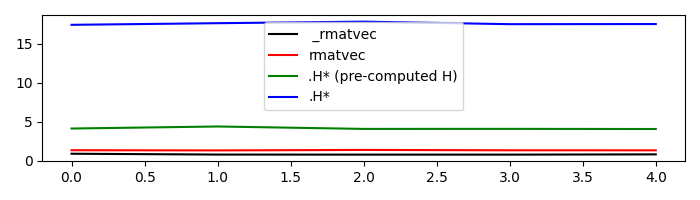
Similarly we now consider the adjoint mode. This can be done in three different ways:

• _rmatvec: directly applies the method implemented for adjoint mode

• rmatvec: performs some checks before and after applying _rmatvec

• .H*: first applies the adjoint .H which creates a new pylops.linearoperator._AdjointLinearOperator` where _matvec and _rmatvec are swapped and then applies the new _matvec.

Once again, after timing these 3 different executions we can see how using _rmatvec (or rmatvec) will result in the faster computation while .H* is very unefficient and slow. Note that if the adjoint has to be applied multiple times it is at least advised to create the adjoint operator by applying .H only once upfront. Not surprisingly, the linear solvers in scipy and PyLops actually use matvec and rmatvec when dealing with linear operators.

# _rmatvec
cmd1 = "Dop._rmatvec(x)"

# rmatvec
cmd2 = "Dop.rmatvec(x)"

# .H* (pre-computed H)
cmd3 = "DopH@x"

# .H*
cmd4 = "Dop.H@x"

# timing
t1 = 1.0e3 * np.array(timeit.repeat(cmd1, setup=cmd_setup, number=500, repeat=5))
t2 = 1.0e3 * np.array(timeit.repeat(cmd2, setup=cmd_setup, number=500, repeat=5))
t3 = 1.0e3 * np.array(timeit.repeat(cmd3, setup=cmd_setup, number=500, repeat=5))
t4 = 1.0e3 * np.array(timeit.repeat(cmd4, setup=cmd_setup, number=500, repeat=5))

plt.figure(figsize=(7, 2))
plt.plot(t1, "k", label=" _rmatvec")
plt.plot(t2, "r", label="rmatvec")
plt.plot(t3, "g", label=".H* (pre-computed H)")
plt.plot(t4, "b", label=".H*")
plt.axis("tight")
plt.legend()
plt.tight_layout()

Just to reiterate once again, it is advised to call matvec and rmatvec unless PyLops linear operators are used for teaching purposes.

We now go through some other methods and special methods that are implemented in pylops.LinearOperator:

• Op1+Op2: maps the special method __add__ and performs summation between two operators and returns a pylops.LinearOperator

• -Op: maps the special method __neg__ and performs negation of an operators and returns a pylops.LinearOperator

• Op1-Op2: maps the special method __sub__ and performs summation between two operators and returns a pylops.LinearOperator

• Op1**N: maps the special method __pow__ and performs exponentiation of an operator and returns a pylops.LinearOperator

• Op/y (and Op.div(y)): maps the special method __truediv__ and performs inversion of an operator

• Op.eigs(): estimates the eigenvalues of the operator

• Op.cond(): estimates the condition number of the operator

• Op.conj(): create complex conjugate operator

Dop = pylops.Diagonal(d)

# +
print(Dop + Dop)

# -
print(-Dop)
print(Dop - 0.5 * Dop)

# **
print(Dop**3)

# * and /
y = Dop @ x
print(Dop / y)

# eigs
print(Dop.eigs(neigs=3))

# cond
print(Dop.cond())

# conj
print(Dop.conj())

<10x10 _SumLinearOperator with dtype=float64>
<10x10 _ScaledLinearOperator with dtype=float64>
<10x10 _SumLinearOperator with dtype=float64>
<10x10 _PowerLinearOperator with dtype=float64>
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[10.+0.j  9.+0.j  8.+0.j]
(9.999999999999991+0j)
<10x10 _ConjLinearOperator with dtype=float64>

To understand the effect of conj we need to look into a problem with an operator in the complex domain. Let’s create again our pylops.Diagonal operator but this time we populate it with complex numbers. We will see that the action of the operator and its complex conjugate is different even if the model is real.

n = 5
d = 1j * (np.arange(n) + 1.0)
x = np.ones(n)
Dop = pylops.Diagonal(d)

print(f"y = Dx = {Dop @ x}")
print(f"y = conj(D)x = {Dop.conj() @ x}")

y = Dx = [0.+1.j 0.+2.j 0.+3.j 0.+4.j 0.+5.j]
y = conj(D)x = [0.-1.j 0.-2.j 0.-3.j 0.-4.j 0.-5.j]

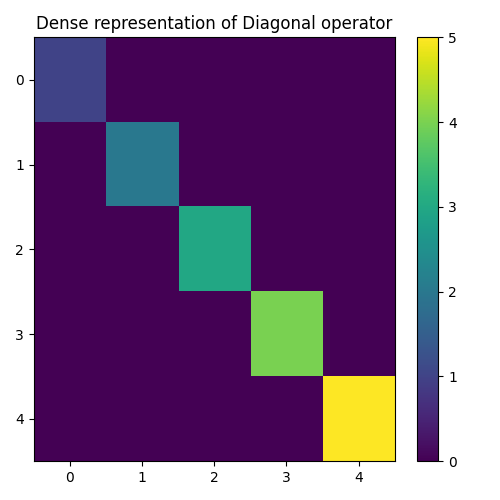
The concept of linear operator may sound abstract. The convenience method pylops.LinearOperator.todense can be used to create the equivalent dense matrix of any operator. In this case for example we expect to see a diagonal matrix with d values along the main diagonal

D = Dop.todense()

plt.figure(figsize=(5, 5))
plt.imshow(np.abs(D))
plt.title("Dense representation of Diagonal operator")
plt.axis("tight")
plt.colorbar()
plt.tight_layout()

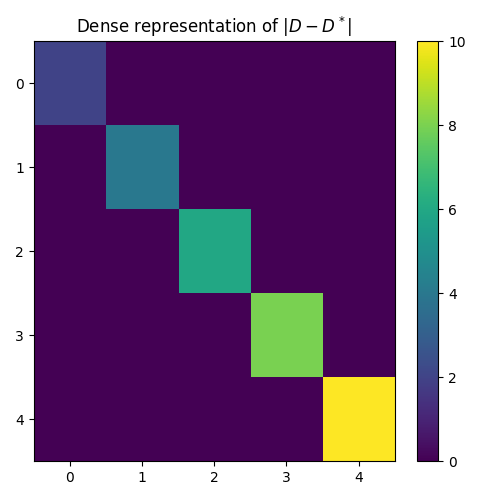
At this point, it is worth reiterating that if two linear operators are combined by means of the algebraical operations shown above, the resulting operator is still a pylops.LinearOperator operator. This means that we can still apply any of the methods implemented in our class like * or /.

Dop1 = Dop - Dop.conj()

y = Dop1 @ x
print(f"x = (Dop - conj(Dop))/y = {Dop1 / y}")

D1 = Dop1.todense()

plt.figure(figsize=(5, 5))
plt.imshow(np.abs(D1))
plt.title(r"Dense representation of $|D - D^*|$")
plt.axis("tight")
plt.colorbar()
plt.tight_layout()

x = (Dop - conj(Dop))/y = [1.+0.j 1.+0.j 1.+0.j 1.+0.j 1.+0.j]

Another important feature of PyLops linear operators is that we can always keep track of how many times the forward and adjoint passes have been applied (and reset when needed). This is particularly useful when running a third party solver to see how many evaluations of our operator are performed inside the solver.

Dop = pylops.Diagonal(d)

y = Dop.matvec(x)
y = Dop.matvec(x)
y = Dop.rmatvec(y)

print(f"Forward evaluations: {Dop.matvec_count}")
print(f"Adjoint evaluations: {Dop.rmatvec_count}")

# Reset
Dop.reset_count()
print(f"Forward evaluations: {Dop.matvec_count}")
print(f"Adjoint evaluations: {Dop.rmatvec_count}")

Forward evaluations: 2
Adjoint evaluations: 1
Forward evaluations: 0
Adjoint evaluations: 0

Finally, let’s consider a case where the pylops.basicoperators.Diagonal operator acts on one dimension of a 2d-array. We will see how in this case the forward and adjoint passes can be applied on the flattened array as well as on the 2d-array directly

#
m, n = 10, 5
d = np.arange(n) + 1.0
x = np.ones((m, n))
Dop = pylops.Diagonal(d, dims=(m, n), axis=-1)

yflat = Dop @ x.ravel()
y = Dop @ x

xadjflat = Dop.H @ yflat
xadj = Dop.H @ y

print(f"yflat shape = {yflat.shape}, y shape = {y.shape}")
print(f"xadjflat shape = {xadjflat.shape}, xadj shape = {xadj.shape}")

yflat shape = (50,), y shape = (10, 5)
xadjflat shape = (50,), xadj shape = (10, 5)

This first tutorial is completed. You have seen the basic operations that can be performed using pylops.LinearOperator and you should now be able to get started combining various PyLops operators and solving your own inverse problems.