19. Automatic Differentiation

This tutorial focuses on the use of pylops.TorchOperator to allow performing Automatic Differentiation (AD) on chains of operators which can be:

• native PyTorch mathematical operations (e.g., torch.log, torch.sin, torch.tan, torch.pow, …)

• neural network operators in torch.nn

• PyLops linear operators

This opens up many opportunities, such as easily including linear regularization terms to nonlinear cost functions or using linear preconditioners with nonlinear modelling operators.

import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
from torch.autograd import gradcheck

import pylops

plt.close("all")
np.random.seed(10)
torch.manual_seed(10)

<torch._C.Generator object at 0x7f8672d2d310>

In this example we consider a simple multidimensional functional:

\[\mathbf{y} = \mathbf{A} sin(\mathbf{x})\]

and we use AD to compute the gradient with respect to the input vector evaluated at \(\mathbf{x}=\mathbf{x}_0\) : \(\mathbf{g} = d\mathbf{y} / d\mathbf{x} |_{\mathbf{x}=\mathbf{x}_0}\).

Let’s start by defining the Jacobian:

\[\begin{split}\textbf{J} = \begin{bmatrix} dy_1 / dx_1 & ... & dy_1 / dx_M \\ ... & ... & ... \\ dy_N / dx_1 & ... & dy_N / dx_M \end{bmatrix} = \begin{bmatrix} a_{11} cos(x_1) & ... & a_{1M} cos(x_M) \\ ... & ... & ... \\ a_{N1} cos(x_1) & ... & a_{NM} cos(x_M) \end{bmatrix} = \textbf{A} cos(\mathbf{x})\end{split}\]

Since both input and output are multidimensional, PyTorch backward actually computes the product between the transposed Jacobian and a vector \(\mathbf{v}\): \(\mathbf{g}=\mathbf{J^T} \mathbf{v}\).

To validate the correctness of the AD result, we can in this simple case also compute the Jacobian analytically and apply it to the same vector \(\mathbf{v}\) that we have provided to PyTorch backward.

nx, ny = 10, 6
x0 = torch.arange(nx, dtype=torch.double, requires_grad=True)

# Forward
A = np.random.normal(0.0, 1.0, (ny, nx))
At = torch.from_numpy(A)
Aop = pylops.TorchOperator(pylops.MatrixMult(A))
y = Aop.apply(torch.sin(x0))

# AD
v = torch.ones(ny, dtype=torch.double)
y.backward(v, retain_graph=True)
adgrad = x0.grad

# Analytical
J = At * torch.cos(x0)
anagrad = torch.matmul(J.T, v)

print("Input: ", x0)
print("AD gradient: ", adgrad)
print("Analytical gradient: ", anagrad)

Input:  tensor([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.], dtype=torch.float64,
       requires_grad=True)
AD gradient:  tensor([ 0.1539, -0.2356,  1.4944, -3.1160, -2.1699,  0.4492,  1.6168,  1.9101,
        -0.4259,  1.7154], dtype=torch.float64)
Analytical gradient:  tensor([ 0.1539, -0.2356,  1.4944, -3.1160, -2.1699,  0.4492,  1.6168,  1.9101,
        -0.4259,  1.7154], dtype=torch.float64, grad_fn=<MvBackward0>)

Similarly we can use the torch.autograd.gradcheck directly from PyTorch. Note that doubles must be used for this to succeed with very small eps and atol

input = (
    torch.arange(nx, dtype=torch.double, requires_grad=True),
    Aop.matvec,
    Aop.rmatvec,
    Aop.device,
    "cpu",
)
test = gradcheck(Aop.Top, input, eps=1e-6, atol=1e-4)
print(test)

True

Note that while matrix-vector multiplication could have been performed using the native PyTorch operator torch.matmul, in this case we have shown that we are also able to use a PyLops operator wrapped in pylops.TorchOperator. As already mentioned, this gives us the ability to use much more complex linear operators provided by PyLops within a chain of mixed linear and nonlinear AD-enabled operators. To conclude, let’s see how we can chain a torch convolutional network with PyLops pylops.Smoothing2D operator. First of all, we consider a single training sample.

class Network(nn.Module):
    def __init__(self, input_channels):
        super(Network, self).__init__()
        self.conv1 = nn.Conv2d(
            input_channels, input_channels // 2, kernel_size=3, padding=1
        )
        self.conv2 = nn.Conv2d(
            input_channels // 2, input_channels // 4, kernel_size=3, padding=1
        )
        self.activation = nn.LeakyReLU(0.2)
        self.maxpool = nn.MaxPool2d(kernel_size=2, stride=2)

    def forward(self, x):
        x = self.conv1(x)
        x = self.activation(x)
        x = self.conv2(x)
        x = self.activation(x)
        return x


net = Network(4)
Cop = pylops.TorchOperator(pylops.Smoothing2D((5, 5), dims=(32, 32)))

# Forward
x = torch.randn(1, 4, 32, 32).requires_grad_()
y = Cop.apply(net(x).view(-1)).reshape(32, 32)

# Backward
loss = y.sum()
loss.backward()

fig, axs = plt.subplots(1, 2, figsize=(12, 3))
axs[0].imshow(y.detach().numpy())
axs[0].set_title("Forward")
axs[0].axis("tight")
axs[1].imshow(x.grad.reshape(4 * 32, 32).T)
axs[1].set_title("Gradient")
axs[1].axis("tight")
plt.tight_layout()

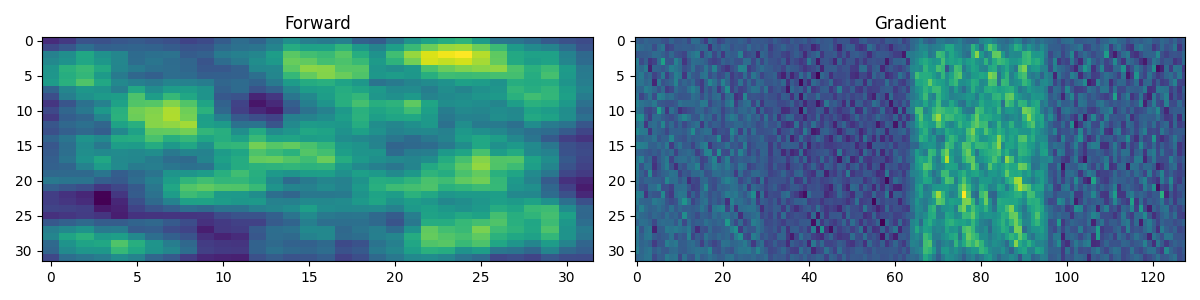
And finally we do the same with a batch of 3 training samples.

net = Network(4)
Cop = pylops.TorchOperator(pylops.Smoothing2D((5, 5), dims=(32, 32)), batch=True)

# Forward
x = torch.randn(3, 4, 32, 32).requires_grad_()
y = Cop.apply(net(x).reshape(3, 32 * 32)).reshape(3, 32, 32)

# Backward
loss = y.sum()
loss.backward()

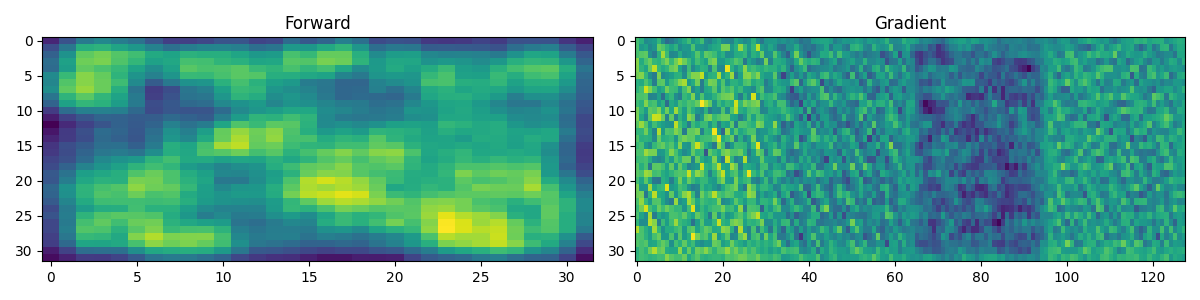
fig, axs = plt.subplots(1, 2, figsize=(12, 3))
axs[0].imshow(y[0].detach().numpy())
axs[0].set_title("Forward")
axs[0].axis("tight")
axs[1].imshow(x.grad[0].reshape(4 * 32, 32).T)
axs[1].set_title("Gradient")
axs[1].axis("tight")
plt.tight_layout()