Note
Go to the end to download the full example code
12. Seismic regularization#
The problem of seismic data regularization (or interpolation) is a very simple one to write, yet ill-posed and very hard to solve.
The forward modelling operator is a simple pylops.Restriction
operator which is applied along the spatial direction(s).
Here \(\mathbf{y} = [\mathbf{y}_{R_1}^T, \mathbf{y}_{R_2}^T,\ldots, \mathbf{y}_{R_N^T}]^T\) where each vector \(\mathbf{y}_{R_i}\) contains all time samples recorded in the seismic data at the specific receiver \(R_i\). Similarly, \(\mathbf{x} = [\mathbf{x}_{r_1}^T, \mathbf{x}_{r_2}^T,\ldots, \mathbf{x}_{r_M}^T]\), contains all traces at the regularly and finely sampled receiver locations \(r_i\).
By inverting such an equation we can create a regularized data with densely and regularly spatial direction(s).
Let’s start by creating a very simple 2d data composed of 3 linear events input parameters
par = {"ox": 0, "dx": 2, "nx": 70, "ot": 0, "dt": 0.004, "nt": 80, "f0": 20}
v = 1500
t0_m = [0.1, 0.2, 0.28]
theta_m = [0, 30, -80]
phi_m = [0]
amp_m = [1.0, -2, 0.5]
# axis
taxis, t2, xaxis, y = makeaxis(par)
# wavelet
wav = ricker(taxis[:41], f0=par["f0"])[0]
# model
_, x = linear2d(xaxis, taxis, v, t0_m, theta_m, amp_m, wav)
We can now define the spatial locations along which the data has been sampled. In this specific example we will assume that we have access only to 40% of the ‘original’ locations.
perc_subsampling = 0.6
nxsub = int(np.round(par["nx"] * perc_subsampling))
iava = np.sort(np.random.permutation(np.arange(par["nx"]))[:nxsub])
# restriction operator
Rop = pylops.Restriction((par["nx"], par["nt"]), iava, axis=0, dtype="float64")
# data
y = Rop * x.ravel()
y = y.reshape(nxsub, par["nt"])
# mask
ymask = Rop.mask(x.ravel())
# inverse
xinv = Rop / y.ravel()
xinv = xinv.reshape(par["nx"], par["nt"])
fig, axs = plt.subplots(1, 2, sharey=True, figsize=(5, 4))
axs[0].imshow(
x.T, cmap="gray", vmin=-2, vmax=2, extent=(xaxis[0], xaxis[-1], taxis[-1], taxis[0])
)
axs[0].set_title("Model")
axs[0].axis("tight")
axs[1].imshow(
ymask.T,
cmap="gray",
vmin=-2,
vmax=2,
extent=(xaxis[0], xaxis[-1], taxis[-1], taxis[0]),
)
axs[1].set_title("Masked model")
axs[1].axis("tight")
plt.tight_layout()
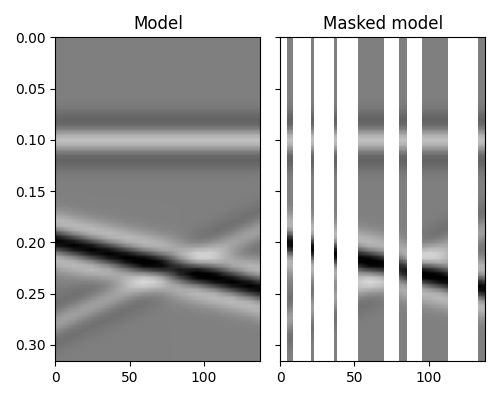
As we can see, inverting the restriction operator is not possible without adding any prior information into the inverse problem. In the following we will consider two possible routes:
regularized inversion with second derivative along the spatial axis
\[J = \|\mathbf{y} - \mathbf{R} \mathbf{x}\|_2 + \epsilon_\nabla ^2 \|\nabla \mathbf{x}\|_2\]sparsity-promoting inversion with
pylops.FFT2operator used as sparsyfing transform\[J = \|\mathbf{y} - \mathbf{R} \mathbf{F}^H \mathbf{x}\|_2 + \epsilon \|\mathbf{F}^H \mathbf{x}\|_1\]
# smooth inversion
D2op = pylops.SecondDerivative((par["nx"], par["nt"]), axis=0, dtype="float64")
xsmooth, _, _ = pylops.waveeqprocessing.SeismicInterpolation(
y,
par["nx"],
iava,
kind="spatial",
**dict(epsRs=[np.sqrt(0.1)], damp=np.sqrt(1e-4), iter_lim=50, show=0)
)
# sparse inversion with FFT2
nfft = 2**8
FFTop = pylops.signalprocessing.FFT2D(
dims=[par["nx"], par["nt"]], nffts=[nfft, nfft], sampling=[par["dx"], par["dt"]]
)
X = FFTop * x.ravel()
X = np.reshape(X, (nfft, nfft))
xl1, Xl1, cost = pylops.waveeqprocessing.SeismicInterpolation(
y,
par["nx"],
iava,
kind="fk",
nffts=(nfft, nfft),
sampling=(par["dx"], par["dt"]),
**dict(niter=50, eps=1e-1)
)
fig, axs = plt.subplots(1, 4, sharey=True, figsize=(13, 4))
axs[0].imshow(
x.T, cmap="gray", vmin=-2, vmax=2, extent=(xaxis[0], xaxis[-1], taxis[-1], taxis[0])
)
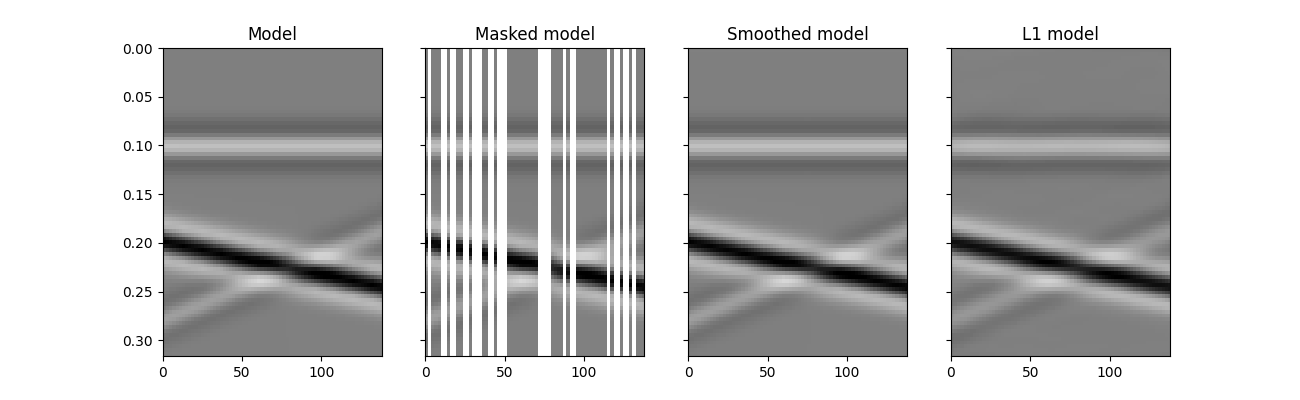
axs[0].set_title("Model")
axs[0].axis("tight")
axs[1].imshow(
ymask.T,
cmap="gray",
vmin=-2,
vmax=2,
extent=(xaxis[0], xaxis[-1], taxis[-1], taxis[0]),
)
axs[1].set_title("Masked model")
axs[1].axis("tight")
axs[2].imshow(
xsmooth.T,
cmap="gray",
vmin=-2,
vmax=2,
extent=(xaxis[0], xaxis[-1], taxis[-1], taxis[0]),
)
axs[2].set_title("Smoothed model")
axs[2].axis("tight")
axs[3].imshow(
xl1.T,
cmap="gray",
vmin=-2,
vmax=2,
extent=(xaxis[0], xaxis[-1], taxis[-1], taxis[0]),
)
axs[3].set_title("L1 model")
axs[3].axis("tight")
fig, axs = plt.subplots(1, 3, figsize=(10, 2))
axs[0].imshow(
np.fft.fftshift(np.abs(X[:, : nfft // 2 - 1]), axes=0).T,
extent=(
np.fft.fftshift(FFTop.f1)[0],
np.fft.fftshift(FFTop.f1)[-1],
FFTop.f2[nfft // 2 - 1],
FFTop.f2[0],
),
)
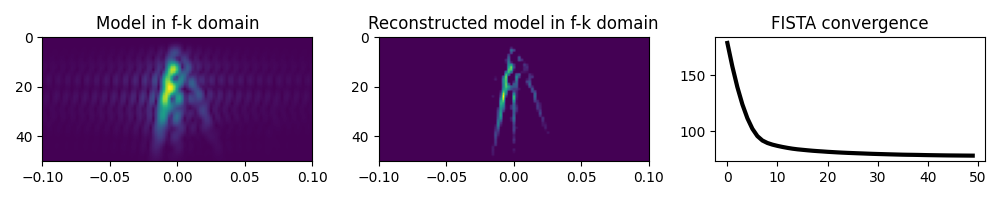
axs[0].set_title("Model in f-k domain")
axs[0].axis("tight")
axs[0].set_xlim(-0.1, 0.1)
axs[0].set_ylim(50, 0)
axs[1].imshow(
np.fft.fftshift(np.abs(Xl1[:, : nfft // 2 - 1]), axes=0).T,
extent=(
np.fft.fftshift(FFTop.f1)[0],
np.fft.fftshift(FFTop.f1)[-1],
FFTop.f2[nfft // 2 - 1],
FFTop.f2[0],
),
)
axs[1].set_title("Reconstructed model in f-k domain")
axs[1].axis("tight")
axs[1].set_xlim(-0.1, 0.1)
axs[1].set_ylim(50, 0)
axs[2].plot(cost, "k", lw=3)
axs[2].set_title("FISTA convergence")
plt.tight_layout()
We see how adding prior information to the inversion can help improving the
estimate of the regularized seismic data. Nevertheless, in both cases the
reconstructed data is not perfect. A better sparsyfing transform could in
fact be chosen here to be the linear
pylops.signalprocessing.Radon2D transform in spite of the
pylops.FFT2 transform.
npx = 40
pxmax = 1e-3
px = np.linspace(-pxmax, pxmax, npx)
Radop = pylops.signalprocessing.Radon2D(taxis, xaxis, px, engine="numba")
RRop = Rop * Radop
# adjoint
Xadj_fromx = Radop.H * x.ravel()
Xadj_fromx = Xadj_fromx.reshape(npx, par["nt"])
Xadj = RRop.H * y.ravel()
Xadj = Xadj.reshape(npx, par["nt"])
# L1 inverse
xl1, Xl1, cost = pylops.waveeqprocessing.SeismicInterpolation(
y,
par["nx"],
iava,
kind="radon-linear",
spataxis=xaxis,
taxis=taxis,
paxis=px,
centeredh=True,
**dict(niter=50, eps=1e-1)
)
fig, axs = plt.subplots(2, 3, sharey=True, figsize=(12, 7))
axs[0][0].imshow(
x.T, cmap="gray", vmin=-2, vmax=2, extent=(xaxis[0], xaxis[-1], taxis[-1], taxis[0])
)
axs[0][0].set_title("Data", fontsize=12)
axs[0][0].axis("tight")
axs[0][1].imshow(
ymask.T,
cmap="gray",
vmin=-2,
vmax=2,
extent=(xaxis[0], xaxis[-1], taxis[-1], taxis[0]),
)
axs[0][1].set_title("Masked data", fontsize=12)
axs[0][1].axis("tight")
axs[0][2].imshow(
xl1.T,
cmap="gray",
vmin=-2,
vmax=2,
extent=(xaxis[0], xaxis[-1], taxis[-1], taxis[0]),
)
axs[0][2].set_title("Reconstructed data", fontsize=12)
axs[0][2].axis("tight")
axs[1][0].imshow(
Xadj_fromx.T,
cmap="gray",
vmin=-70,
vmax=70,
extent=(px[0], px[-1], taxis[-1], taxis[0]),
)
axs[1][0].set_title("Adj. Radon on data", fontsize=12)
axs[1][0].axis("tight")
axs[1][1].imshow(
Xadj.T, cmap="gray", vmin=-50, vmax=50, extent=(px[0], px[-1], taxis[-1], taxis[0])
)
axs[1][1].set_title("Adj. Radon on subsampled data", fontsize=12)
axs[1][1].axis("tight")
axs[1][2].imshow(
Xl1.T, cmap="gray", vmin=-0.2, vmax=0.2, extent=(px[0], px[-1], taxis[-1], taxis[0])
)
axs[1][2].set_title("Inverse Radon on subsampled data", fontsize=12)
axs[1][2].axis("tight")
plt.tight_layout()
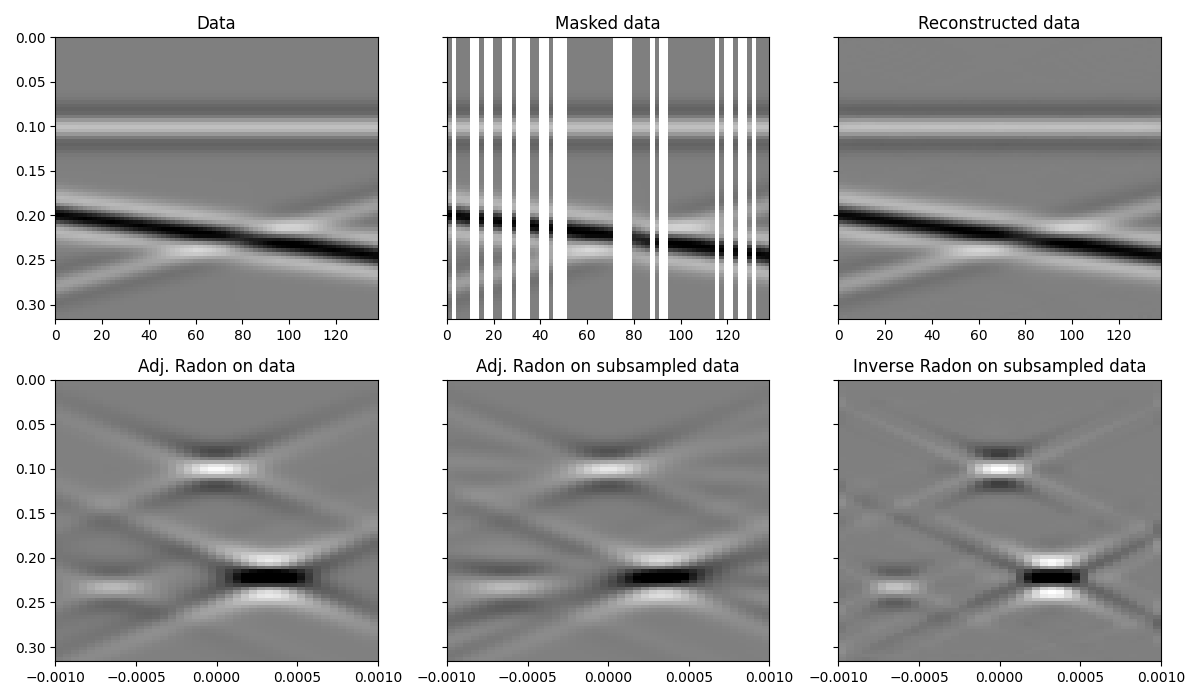
Finally, let’s take now a more realistic dataset. We will use once again the
linear pylops.signalprocessing.Radon2D transform but we will
take advantnge of the pylops.signalprocessing.Sliding2D operator
to perform such a transform locally instead of globally to the entire
dataset.
inputfile = "../testdata/marchenko/input.npz"
inputdata = np.load(inputfile)
x = inputdata["R"][50, :, ::2]
x = x / np.abs(x).max()
taxis, xaxis = inputdata["t"][::2], inputdata["r"][0]
par = {}
par["nx"], par["nt"] = x.shape
par["dx"] = inputdata["r"][0, 1] - inputdata["r"][0, 0]
par["dt"] = inputdata["t"][1] - inputdata["t"][0]
# add wavelet
wav = inputdata["wav"][::2]
wav_c = np.argmax(wav)
x = np.apply_along_axis(convolve, 1, x, wav, mode="full")
x = x[:, wav_c:][:, : par["nt"]]
# gain
gain = np.tile((taxis**2)[:, np.newaxis], (1, par["nx"])).T
x = x * gain
# subsampling locations
perc_subsampling = 0.5
Nsub = int(np.round(par["nx"] * perc_subsampling))
iava = np.sort(np.random.permutation(np.arange(par["nx"]))[:Nsub])
# restriction operator
Rop = pylops.Restriction((par["nx"], par["nt"]), iava, axis=0, dtype="float64")
y = Rop * x.ravel()
xadj = Rop.H * y.ravel()
y = y.reshape(Nsub, par["nt"])
xadj = xadj.reshape(par["nx"], par["nt"])
# apply mask
ymask = Rop.mask(x.ravel())
# sliding windows with radon transform
dx = par["dx"]
nwins = 4
nwin = 27
nover = 3
npx = 31
pxmax = 5e-4
px = np.linspace(-pxmax, pxmax, npx)
dimsd = x.shape
dims = (nwins * npx, dimsd[1])
Op = pylops.signalprocessing.Radon2D(
taxis,
np.linspace(-par["dx"] * nwin // 2, par["dx"] * nwin // 2, nwin),
px,
centeredh=True,
kind="linear",
engine="numba",
)
Slidop = pylops.signalprocessing.Sliding2D(
Op, dims, dimsd, nwin, nover, tapertype="cosine"
)
# adjoint
RSop = Rop * Slidop
Xadj_fromx = Slidop.H * x.ravel()
Xadj_fromx = Xadj_fromx.reshape(npx * nwins, par["nt"])
Xadj = RSop.H * y.ravel()
Xadj = Xadj.reshape(npx * nwins, par["nt"])
# inverse
xl1, Xl1, _ = pylops.waveeqprocessing.SeismicInterpolation(
y,
par["nx"],
iava,
kind="sliding",
spataxis=xaxis,
taxis=taxis,
paxis=px,
nwins=nwins,
nwin=nwin,
nover=nover,
**dict(niter=50, eps=1e-2)
)
fig, axs = plt.subplots(2, 3, sharey=True, figsize=(12, 14))
axs[0][0].imshow(
x.T,
cmap="gray",
vmin=-0.1,
vmax=0.1,
extent=(xaxis[0], xaxis[-1], taxis[-1], taxis[0]),
)
axs[0][0].set_title("Data")
axs[0][0].axis("tight")
axs[0][1].imshow(
ymask.T,
cmap="gray",
vmin=-0.1,
vmax=0.1,
extent=(xaxis[0], xaxis[-1], taxis[-1], taxis[0]),
)
axs[0][1].set_title("Masked data")
axs[0][1].axis("tight")
axs[0][2].imshow(
xl1.T,
cmap="gray",
vmin=-0.1,
vmax=0.1,
extent=(xaxis[0], xaxis[-1], taxis[-1], taxis[0]),
)
axs[0][2].set_title("Reconstructed data")
axs[0][2].axis("tight")
axs[1][0].imshow(
Xadj_fromx.T,
cmap="gray",
vmin=-1,
vmax=1,
extent=(px[0], px[-1], taxis[-1], taxis[0]),
)
axs[1][0].set_title("Adjoint Radon on data")
axs[1][0].axis("tight")
axs[1][1].imshow(
Xadj.T,
cmap="gray",
vmin=-0.6,
vmax=0.6,
extent=(px[0], px[-1], taxis[-1], taxis[0]),
)
axs[1][1].set_title("Adjoint Radon on subsampled data")
axs[1][1].axis("tight")
axs[1][2].imshow(
Xl1.T,
cmap="gray",
vmin=-0.03,
vmax=0.03,
extent=(px[0], px[-1], taxis[-1], taxis[0]),
)
axs[1][2].set_title("Inverse Radon on subsampled data")
axs[1][2].axis("tight")
plt.tight_layout()
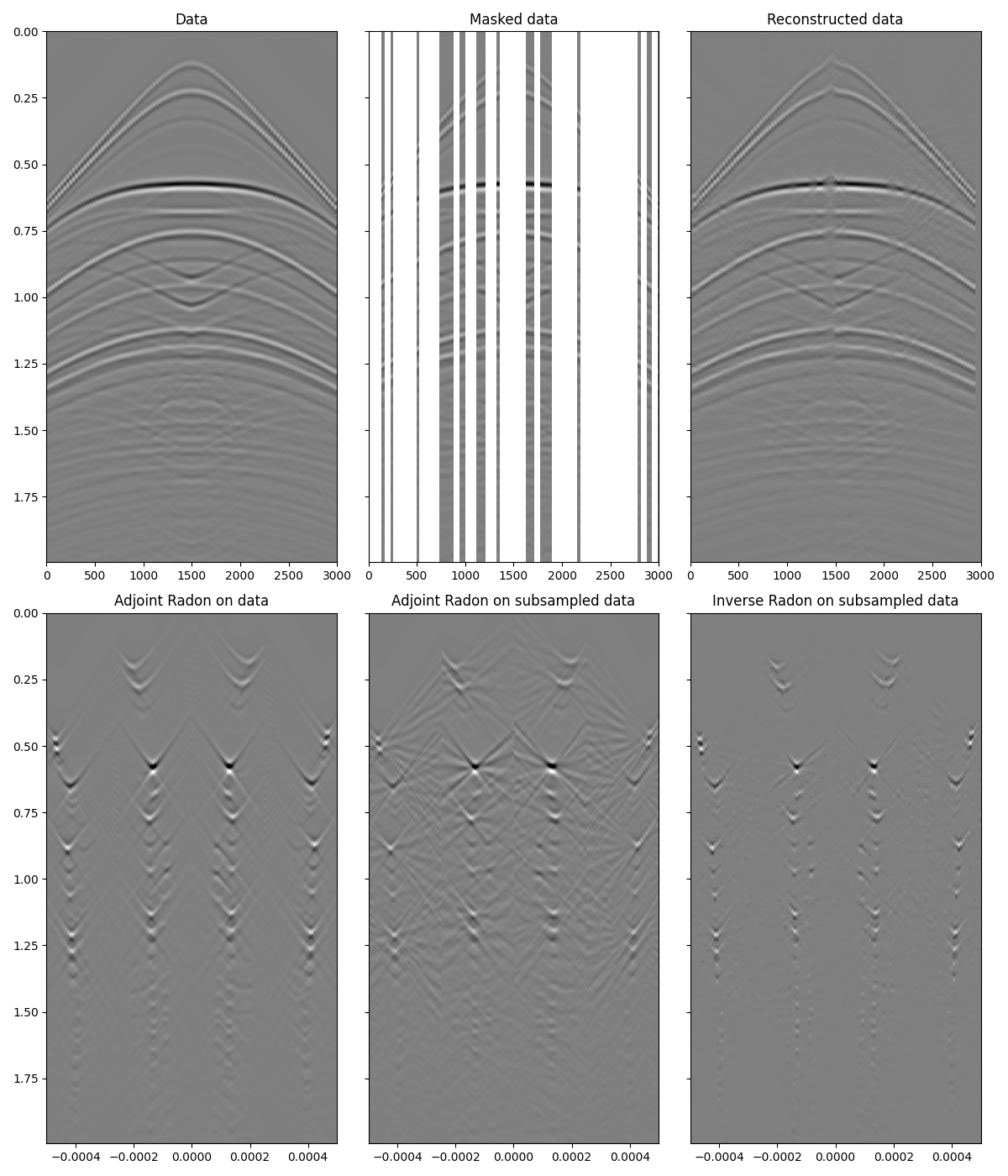
As expected the linear pylops.signalprocessing.Radon2D is
able to locally explain events in the input data and leads to a satisfactory
recovery. Note that increasing the number of iterations and sliding windows
can further refine the result, especially the accuracy of weak events, as
shown in this companion
notebook.
Total running time of the script: (0 minutes 9.003 seconds)