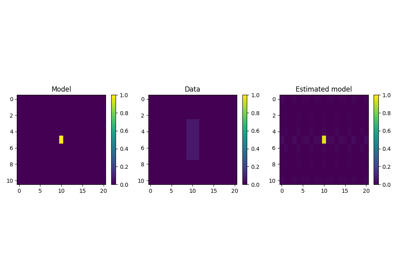
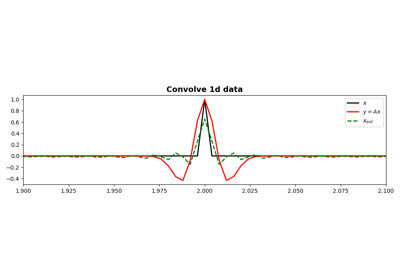
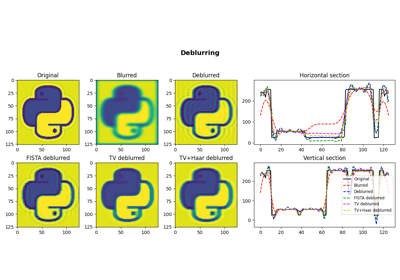
pylops.signalprocessing.ConvolveND#
- class pylops.signalprocessing.ConvolveND(dims, h, offset=None, axes=(-2, -1), method='fft', dtype='float64', name='C')[source]#
ND convolution operator.
Apply n-dimensional convolution with a compact filter to model (and data) along the
axesof a n-dimensional array.- Parameters
- dims
listorint Number of samples for each dimension
- h
numpy.ndarray nd compact filter to be convolved to input signal
- offset
tuple, optional Indices of the center of the compact filter
- axes
int, optional New in version 2.0.0.
Axes along which convolution is applied
- method
str, optional Method used to calculate the convolution (
directorfft).- dtype
str, optional Type of elements in input array.
- name
str, optional New in version 2.0.0.
Name of operator (to be used by
pylops.utils.describe.describe)
- dims
Notes
The ConvolveND operator applies n-dimensional convolution between the input signal \(d(x_1, x_2, ..., x_N)\) and a compact filter kernel \(h(x_1, x_2, ..., x_N)\) in forward model. This is a straighforward extension to multiple dimensions of
pylops.signalprocessing.Convolve2Doperator.- Attributes
- shape
tuple Operator shape
- explicit
bool Operator contains a matrix that can be solved explicitly (
True) or not (False)
- shape
Methods
__init__(dims, h[, offset, axes, method, ...])adjoint()apply_columns(cols)Apply subset of columns of operator
cond([uselobpcg])Condition number of linear operator.
conj()Complex conjugate operator
div(y[, niter, densesolver])Solve the linear problem \(\mathbf{y}=\mathbf{A}\mathbf{x}\).
dot(x)Matrix-matrix or matrix-vector multiplication.
eigs([neigs, symmetric, niter, uselobpcg])Most significant eigenvalues of linear operator.
matmat(X)Matrix-matrix multiplication.
matvec(x)Matrix-vector multiplication.
reset_count()Reset counters
rmatmat(X)Matrix-matrix multiplication.
rmatvec(x)Adjoint matrix-vector multiplication.
todense([backend])Return dense matrix.
toimag([forw, adj])Imag operator
toreal([forw, adj])Real operator
tosparse()Return sparse matrix.
trace([neval, method, backend])Trace of linear operator.
transpose()