02. The Dot-Test

One of the most important aspect of writing a Linear operator is to be able to verify that the code implemented in forward mode and the code implemented in adjoint mode are effectively adjoint to each other. If this is the case, your Linear operator will successfully pass the so-called dot-test. Refer to the Notes section of pylops.utils.dottest) for a more detailed description.

In this example, I will show you how to use the dot-test for a variety of operator when model and data are either real or complex numbers.

import matplotlib.gridspec as pltgs
import matplotlib.pyplot as plt

# pylint: disable=C0103
import numpy as np

import pylops
from pylops.utils import dottest

plt.close("all")

Let’s start with something very simple. We will make a pylops.MatrixMult operator and verify that its implementation passes the dot-test. For this time, we will do this step-by-step, replicating what happens in the pylops.utils.dottest routine.

N, M = 5, 3
Mat = np.arange(N * M).reshape(N, M)
Op = pylops.MatrixMult(Mat)

v = np.random.randn(N)
u = np.random.randn(M)

# Op * u
y = Op.matvec(u)
# Op'* v
x = Op.rmatvec(v)

yy = np.dot(y, v)  # (Op  * u)' * v
xx = np.dot(u, x)  # u' * (Op' * v)

print(f"Dot-test {np.abs((yy - xx) / ((yy + xx + 1e-15) / 2)):.2e}")

Dot-test 1.37e-16

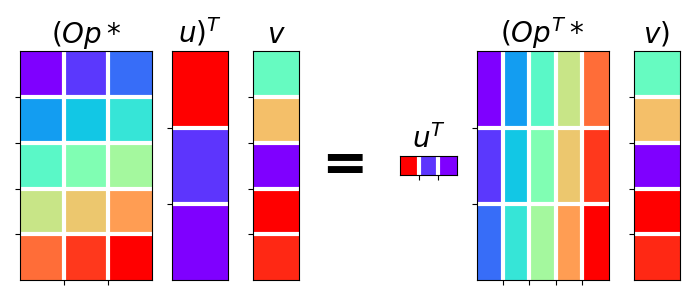
And here is a visual intepretation of what a dot-test is

gs = pltgs.GridSpec(1, 9)
fig = plt.figure(figsize=(7, 3))
ax = plt.subplot(gs[0, 0:2])
ax.imshow(Op.A, cmap="rainbow")
ax.set_title(r"$(Op*$", size=20, fontweight="bold")
ax.set_xticks(np.arange(M - 1) + 0.5)
ax.set_yticks(np.arange(N - 1) + 0.5)
ax.grid(linewidth=3, color="white")
ax.xaxis.set_ticklabels([])
ax.yaxis.set_ticklabels([])
ax.axis("tight")
ax = plt.subplot(gs[0, 2])
ax.imshow(u[:, np.newaxis], cmap="rainbow")
ax.set_title(r"$u)^T$", size=20, fontweight="bold")
ax.set_xticks([])
ax.set_yticks(np.arange(M - 1) + 0.5)
ax.grid(linewidth=3, color="white")
ax.xaxis.set_ticklabels([])
ax.yaxis.set_ticklabels([])
ax.axis("tight")
ax = plt.subplot(gs[0, 3])
ax.imshow(v[:, np.newaxis], cmap="rainbow")
ax.set_title(r"$v$", size=20, fontweight="bold")
ax.set_xticks([])
ax.set_yticks(np.arange(N - 1) + 0.5)
ax.grid(linewidth=3, color="white")
ax.xaxis.set_ticklabels([])
ax.yaxis.set_ticklabels([])
ax = plt.subplot(gs[0, 4])
ax.text(
    0.35,
    0.5,
    "=",
    horizontalalignment="center",
    verticalalignment="center",
    size=40,
    fontweight="bold",
)
ax.axis("off")
ax = plt.subplot(gs[0, 5])
ax.imshow(u[:, np.newaxis].T, cmap="rainbow")
ax.set_title(r"$u^T$", size=20, fontweight="bold")
ax.set_xticks(np.arange(M - 1) + 0.5)
ax.set_yticks([])
ax.grid(linewidth=3, color="white")
ax.xaxis.set_ticklabels([])
ax.yaxis.set_ticklabels([])
ax = plt.subplot(gs[0, 6:8])
ax.imshow(Op.A.T, cmap="rainbow")
ax.set_title(r"$(Op^T*$", size=20, fontweight="bold")
ax.set_xticks(np.arange(N - 1) + 0.5)
ax.set_yticks(np.arange(M - 1) + 0.5)
ax.grid(linewidth=3, color="white")
ax.xaxis.set_ticklabels([])
ax.yaxis.set_ticklabels([])
ax.axis("tight")
ax = plt.subplot(gs[0, 8])
ax.imshow(v[:, np.newaxis], cmap="rainbow")
ax.set_title(r"$v)$", size=20, fontweight="bold")
ax.set_xticks([])
ax.set_yticks(np.arange(N - 1) + 0.5)
ax.grid(linewidth=3, color="white")
ax.xaxis.set_ticklabels([])
ax.yaxis.set_ticklabels([])
plt.tight_layout()

From now on, we can simply use the pylops.utils.dottest implementation of the dot-test and pass the operator we would like to validate, its size in the model and data spaces and optionally the tolerance we will be accepting for the dot-test to be considered succesfull. Finally we need to specify if our data or/and model vectors contain complex numbers using the complexflag parameter. While the dot-test will return True when succesfull and False otherwise, we can also ask to print its outcome putting the verb parameters to True.

N = 10
d = np.arange(N)
Dop = pylops.Diagonal(d)

_ = dottest(Dop, N, N, rtol=1e-6, complexflag=0, verb=True)

Dot test passed, v^H(Opu)=-6.91965436475742 - u^H(Op^Hv)=-6.91965436475742

We move now to a more complicated operator, the pylops.signalprocessing.FFT operator. We use once again the pylops.utils.dottest to verify its implementation and since we are dealing with a transform that can be applied to both real and complex array, we try different combinations using the complexflag input.

dt = 0.005
nt = 100
nfft = 2**10

FFTop = pylops.signalprocessing.FFT(
    dims=(nt,), nfft=nfft, sampling=dt, dtype=np.complex128
)
dottest(FFTop, nfft, nt, complexflag=2, verb=True)
_ = dottest(FFTop, nfft, nt, complexflag=3, verb=True)

Dot test passed, v^H(Opu)=(-17.13910350422714+3.8288339959112507j) - u^H(Op^Hv)=(-17.139103504227144+3.8288339959112494j)
Dot test passed, v^H(Opu)=(11.42080013111478-3.688151329246325j) - u^H(Op^Hv)=(11.420800131114781-3.6881513292463266j)