Note
Go to the end to download the full example code
16. CT Scan Imaging#
This tutorial considers a very well-known inverse problem from the field of medical imaging.
We will be using the pylops.signalprocessing.Radon2D operator
to model a sinogram, which is a graphic representation of the raw data
obtained from a CT scan. The sinogram is further inverted using both a L2
solver and a TV-regularized solver like Split-Bregman.
import matplotlib.pyplot as plt
# sphinx_gallery_thumbnail_number = 2
import numpy as np
from numba import jit
import pylops
plt.close("all")
np.random.seed(10)
Let’s start by loading the Shepp-Logan phantom model. We can then construct
the sinogram by providing a custom-made function to the
pylops.signalprocessing.Radon2D that samples parametric curves of
such a type:
where \(\theta\) is the angle between the x-axis (\(x\)) and the perpendicular to the summation line and \(r\) is the distance from the origin of the summation line. Radon transform in CT corresponds to the integral of the input image along the straight line above. To implement the integration in PyLops we simply need to express \(t(r,\theta;x)\) which is given by:
Note that in the above implementation we added centering \(t \mapsto t - n_y/2\) and
\(r \mapsto r - n_y/2\) so that the origin of the integration lines is exactly in the
center of the image (centering for \(x\) is not needed because we will use
centeredh=True in the constructor of Radon2D).
x = np.load("../testdata/optimization/shepp_logan_phantom.npy").T
x = x / x.max()
nx, ny = x.shape
ntheta = 151
theta = np.linspace(0.0, np.pi, ntheta, endpoint=False)
RLop = pylops.signalprocessing.Radon2D(
np.arange(ny),
np.arange(nx),
theta,
kind=radoncurve,
centeredh=True,
interp=False,
engine="numba",
dtype="float64",
)
y = RLop.H * x
We can now first perform the adjoint, which in the medical imaging literature is also referred to as back-projection.
This is the first step of a common reconstruction technique, named filtered back-projection, which simply applies a correction filter in the frequency domain to the adjoint model.
xrec = RLop * y
fig, axs = plt.subplots(1, 3, figsize=(10, 4))
axs[0].imshow(x.T, vmin=0, vmax=1, cmap="gray")
axs[0].set_title("Model")
axs[0].axis("tight")
axs[1].imshow(y.T, cmap="gray")
axs[1].set_title("Data")
axs[1].axis("tight")
axs[2].imshow(xrec.T, cmap="gray")
axs[2].set_title("Adjoint model in PyLops")
axs[2].axis("tight")
fig.tight_layout()
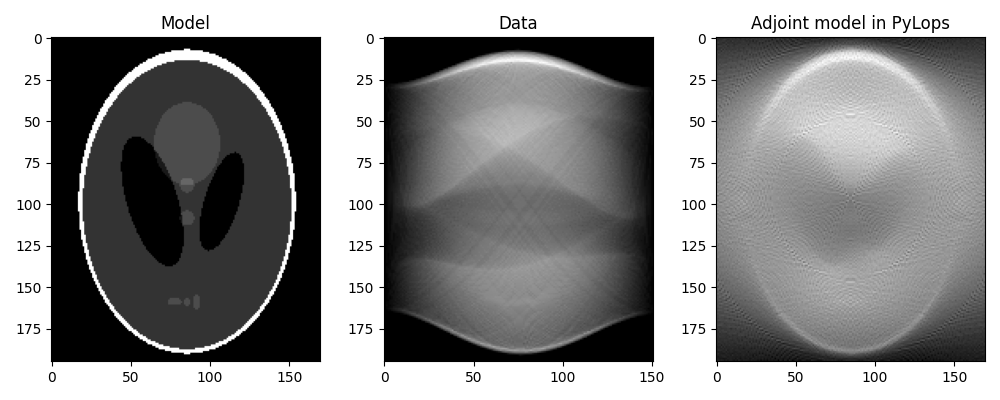
Note that our raw data y does not represent exactly classical sinograms
in medical imaging. Integration along curves in the adjoint form of
pylops.signalprocessing.Radon2D is performed with respect to
\(dx\), whereas canonically it is assumed to be with respect to the natural
parametrization \(dl = \sqrt{(dx)^2 + (dt)^2}\). To retrieve back the
classical sinogram we have to divide data by the jacobian
\(j(x,l) = \left\vert dx/dl \right\vert = |\sin(\theta)|\).
sinogram = np.divide(
y.T, np.abs(np.sin(theta) + 1e-15)
) # small shift to avoid zero-division
fig, axs = plt.subplots(1, 2, figsize=(10, 4))
axs[0].imshow(y.T, cmap="gray")
axs[0].set_title("Data")
axs[0].axis("tight")
axs[1].imshow(sinogram, cmap="gray")
axs[1].set_title("Sinogram in medical imaging")
axs[1].axis("tight")
fig.tight_layout()
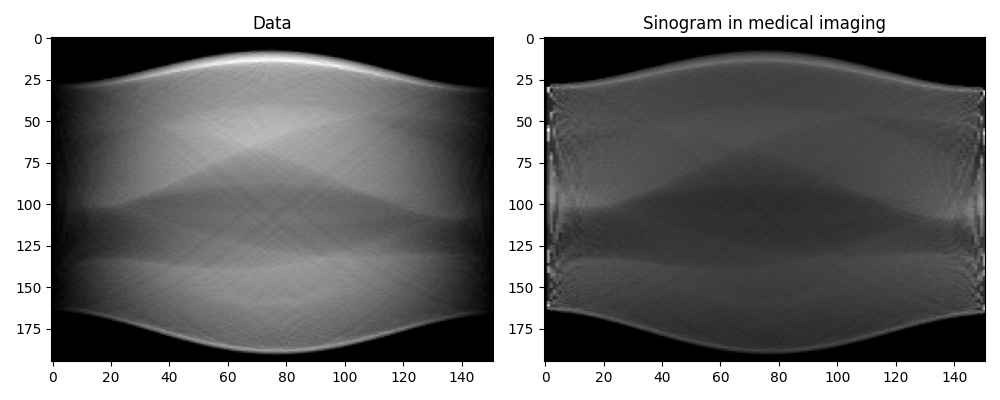
From now on, we will not pursue further working with the “true sinogram”, instead
we will reconstruct the original phantom directly from y. For this we take advantage
of our different solvers and try to invert the modelling operator both in a
least-squares sense and using TV-reg.
Dop = [
pylops.FirstDerivative(
(nx, ny), axis=0, edge=True, kind="backward", dtype=np.float64
),
pylops.FirstDerivative(
(nx, ny), axis=1, edge=True, kind="backward", dtype=np.float64
),
]
D2op = pylops.Laplacian(dims=(nx, ny), edge=True, dtype=np.float64)
# L2
xinv_sm = pylops.optimization.leastsquares.regularized_inversion(
RLop.H, y.ravel(), [D2op], epsRs=[1e1], **dict(iter_lim=20)
)[0]
xinv_sm = np.real(xinv_sm.reshape(nx, ny))
# TV
mu = 1.5
lamda = [1.0, 1.0]
niter = 3
niterinner = 4
xinv = pylops.optimization.sparsity.splitbregman(
RLop.H,
y.ravel(),
Dop,
niter_outer=niter,
niter_inner=niterinner,
mu=mu,
epsRL1s=lamda,
tol=1e-4,
tau=1.0,
show=False,
**dict(iter_lim=20, damp=1e-2)
)[0]
xinv = np.real(xinv.reshape(nx, ny))
fig, axs = plt.subplots(1, 3, figsize=(10, 4))
axs[0].imshow(x.T, vmin=0, vmax=1, cmap="gray")
axs[0].set_title("Model")
axs[0].axis("tight")
axs[1].imshow(xinv_sm.T, vmin=0, vmax=1, cmap="gray")
axs[1].set_title("L2 Inversion")
axs[1].axis("tight")
axs[2].imshow(xinv.T, vmin=0, vmax=1, cmap="gray")
axs[2].set_title("TV-Reg Inversion")
axs[2].axis("tight")
fig.tight_layout()
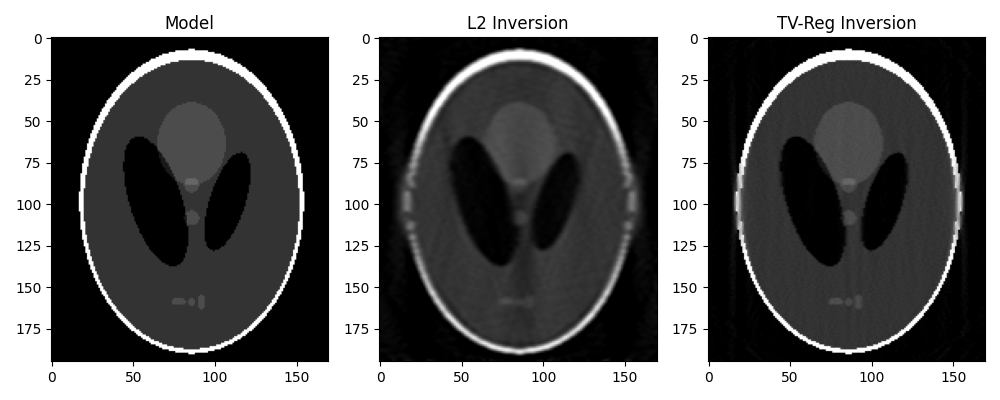
Total running time of the script: (0 minutes 16.061 seconds)