pylops.Smoothing1D#
- class pylops.Smoothing1D(nsmooth, dims, axis=-1, dtype='float64', name='S')[source]#
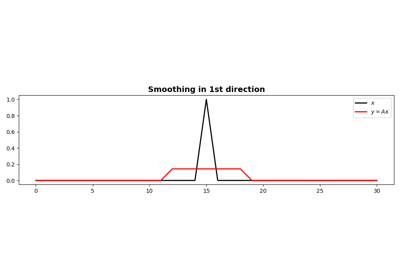
1D Smoothing.
Apply smoothing to model (and data) to a multi-dimensional array along
axis.- Parameters
- nsmooth
int Length of smoothing operator (must be odd)
- dims
tupleorint Number of samples for each dimension
- axis
int, optional New in version 2.0.0.
Axis along which model (and data) are smoothed.
- dtype
str, optional Type of elements in input array.
- nsmooth
Notes
The Smoothing1D operator is a special type of convolutional operator that convolves the input model (or data) with a constant filter of size \(n_\text{smooth}\):
\[\mathbf{f} = [ 1/n_\text{smooth}, 1/n_\text{smooth}, ..., 1/n_\text{smooth} ]\]When applied to the first direction:
\[y[i,j,k] = 1/n_\text{smooth} \sum_{l=-(n_\text{smooth}-1)/2}^{(n_\text{smooth}-1)/2} x[l,j,k]\]Similarly when applied to the second direction:
\[y[i,j,k] = 1/n_\text{smooth} \sum_{l=-(n_\text{smooth}-1)/2}^{(n_\text{smooth}-1)/2} x[i,l,k]\]and the third direction:
\[y[i,j,k] = 1/n_\text{smooth} \sum_{l=-(n_\text{smooth}-1)/2}^{(n_\text{smooth}-1)/2} x[i,j,l]\]Note that since the filter is symmetrical, the Smoothing1D operator is self-adjoint.
- Attributes
- shape
tuple Operator shape
- explicit
bool Operator contains a matrix that can be solved explicitly (
True) or not (False)
- shape
Methods
__init__(nsmooth, dims[, axis, dtype, name])adjoint()apply_columns(cols)Apply subset of columns of operator
cond([uselobpcg])Condition number of linear operator.
conj()Complex conjugate operator
div(y[, niter, densesolver])Solve the linear problem \(\mathbf{y}=\mathbf{A}\mathbf{x}\).
dot(x)Matrix-matrix or matrix-vector multiplication.
eigs([neigs, symmetric, niter, uselobpcg])Most significant eigenvalues of linear operator.
matmat(X)Matrix-matrix multiplication.
matvec(x)Matrix-vector multiplication.
reset_count()Reset counters
rmatmat(X)Matrix-matrix multiplication.
rmatvec(x)Adjoint matrix-vector multiplication.
todense([backend])Return dense matrix.
toimag([forw, adj])Imag operator
toreal([forw, adj])Real operator
tosparse()Return sparse matrix.
trace([neval, method, backend])Trace of linear operator.
transpose()