Note
Go to the end to download the full example code
Symmetrize#
This example shows how to use the pylops.Symmetrize
operator which takes an input signal and returns a symmetric signal
by pre-pending the input signal in reversed order. Such an operation can be
inverted as we will see in this example.
Moreover the pylops.Symmetrize can be used as preconditioning
to any inverse problem where we are after inverting for a signal that we
want to ensure is symmetric. Refer to Wavelet estimation
for an example of such a type.
import matplotlib.pyplot as plt
import numpy as np
import pylops
plt.close("all")
Let’s start with a 1D example. Define an input signal composed of
nt samples
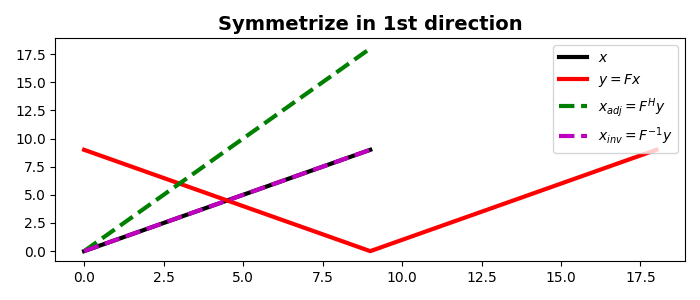
We can now create our flip operator and apply it to the input signal. We can also apply the adjoint to the flipped signal and we can see how for this operator the adjoint is effectively equivalent to the inverse.
Sop = pylops.Symmetrize(nt)
y = Sop * x
xadj = Sop.H * y
xinv = Sop / y
plt.figure(figsize=(7, 3))
plt.plot(x, "k", lw=3, label=r"$x$")
plt.plot(y, "r", lw=3, label=r"$y=Fx$")
plt.plot(xadj, "--g", lw=3, label=r"$x_{adj} = F^H y$")
plt.plot(xinv, "--m", lw=3, label=r"$x_{inv} = F^{-1} y$")
plt.title("Symmetrize in 1st direction", fontsize=14, fontweight="bold")
plt.legend()
plt.tight_layout()
Let’s now repeat the same exercise on a two dimensional signal. We will first flip the model along the first axis and then along the second axis
nt, nx = 10, 6
x = np.outer(np.arange(nt), np.ones(nx))
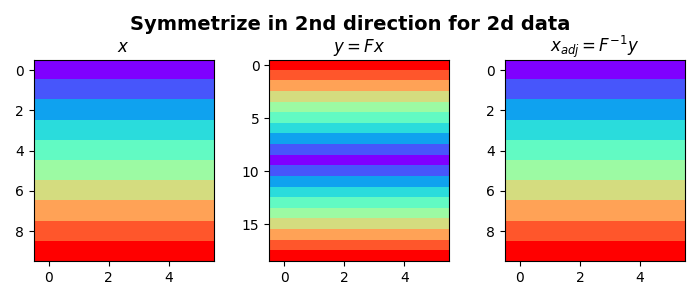
Sop = pylops.Symmetrize((nt, nx), axis=0)
y = Sop * x
xadj = Sop.H * y
xinv = Sop / y.ravel()
xinv = xinv.reshape(Sop.dims)
fig, axs = plt.subplots(1, 3, figsize=(7, 3))
fig.suptitle(
"Symmetrize in 2nd direction for 2d data", fontsize=14, fontweight="bold", y=0.95
)
axs[0].imshow(x, cmap="rainbow", vmin=0, vmax=9)
axs[0].set_title(r"$x$")
axs[0].axis("tight")
axs[1].imshow(y, cmap="rainbow", vmin=0, vmax=9)
axs[1].set_title(r"$y=Fx$")
axs[1].axis("tight")
axs[2].imshow(xinv, cmap="rainbow", vmin=0, vmax=9)
axs[2].set_title(r"$x_{adj}=F^{-1}y$")
axs[2].axis("tight")
plt.tight_layout()
plt.subplots_adjust(top=0.8)
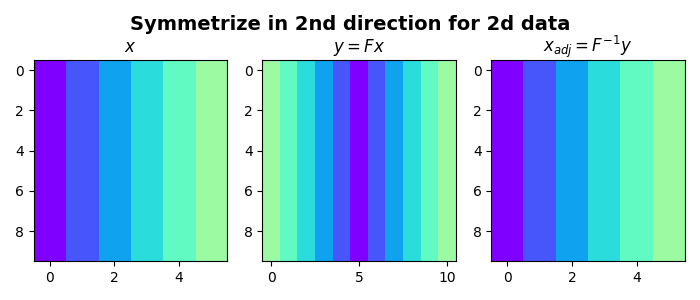
x = np.outer(np.ones(nt), np.arange(nx))
Sop = pylops.Symmetrize((nt, nx), axis=1)
y = Sop * x
xadj = Sop.H * y
xinv = Sop / y.ravel()
xinv = xinv.reshape(Sop.dims)
# sphinx_gallery_thumbnail_number = 3
fig, axs = plt.subplots(1, 3, figsize=(7, 3))
fig.suptitle(
"Symmetrize in 2nd direction for 2d data", fontsize=14, fontweight="bold", y=0.95
)
axs[0].imshow(x, cmap="rainbow", vmin=0, vmax=9)
axs[0].set_title(r"$x$")
axs[0].axis("tight")
axs[1].imshow(y, cmap="rainbow", vmin=0, vmax=9)
axs[1].set_title(r"$y=Fx$")
axs[1].axis("tight")
axs[2].imshow(xinv, cmap="rainbow", vmin=0, vmax=9)
axs[2].set_title(r"$x_{adj}=F^{-1}y$")
axs[2].axis("tight")
plt.tight_layout()
plt.subplots_adjust(top=0.8)
Total running time of the script: (0 minutes 1.028 seconds)