Note
Go to the end to download the full example code
Zero#
This example shows how to use the pylops.basicoperators.Zero operator.
This operators simply zeroes the data in forward mode and the model in adjoint mode.
import matplotlib.gridspec as pltgs
import matplotlib.pyplot as plt
import numpy as np
import pylops
plt.close("all")
Let’s define an zero operator \(\mathbf{0}\) with same number of elements for data \(N\) and model \(M\).
N, M = 5, 5
x = np.arange(M)
Zop = pylops.basicoperators.Zero(M, dtype="int")
y = Zop * x
xadj = Zop.H * y
gs = pltgs.GridSpec(1, 6)
fig = plt.figure(figsize=(7, 4))
ax = plt.subplot(gs[0, 0:3])
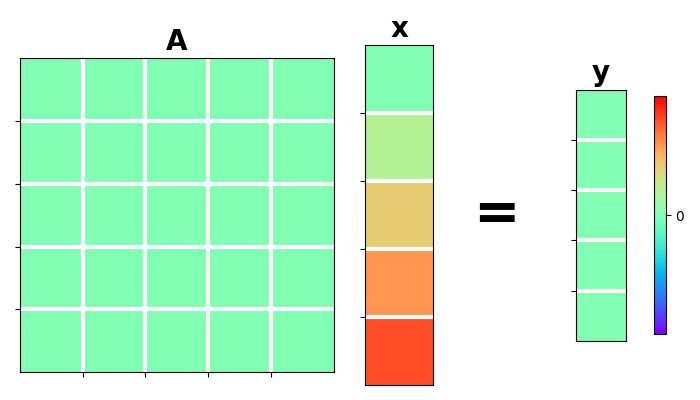
ax.imshow(np.zeros((N, N)), cmap="rainbow", vmin=-M, vmax=M)
ax.set_title("A", size=20, fontweight="bold")
ax.set_xticks(np.arange(N - 1) + 0.5)
ax.set_yticks(np.arange(M - 1) + 0.5)
ax.grid(linewidth=3, color="white")
ax.xaxis.set_ticklabels([])
ax.yaxis.set_ticklabels([])
ax = plt.subplot(gs[0, 3])
im = ax.imshow(x[:, np.newaxis], cmap="rainbow", vmin=-M, vmax=M)
ax.set_title("x", size=20, fontweight="bold")
ax.set_xticks([])
ax.set_yticks(np.arange(M - 1) + 0.5)
ax.grid(linewidth=3, color="white")
ax.xaxis.set_ticklabels([])
ax.yaxis.set_ticklabels([])
ax = plt.subplot(gs[0, 4])
ax.text(
0.35,
0.5,
"=",
horizontalalignment="center",
verticalalignment="center",
size=40,
fontweight="bold",
)
ax.axis("off")
ax = plt.subplot(gs[0, 5])
ax.imshow(y[:, np.newaxis], cmap="rainbow", vmin=-M, vmax=M)
ax.set_title("y", size=20, fontweight="bold")
ax.set_xticks([])
ax.set_yticks(np.arange(N - 1) + 0.5)
ax.grid(linewidth=3, color="white")
ax.xaxis.set_ticklabels([])
ax.yaxis.set_ticklabels([])
fig.colorbar(im, ax=ax, ticks=[0], pad=0.3, shrink=0.7)
plt.tight_layout()
Similarly we can consider the case with data bigger than model
x = [0 1 2 3 4]
0*x = [0 0 0 0 0 0 0 0 0 0]
0'*y = [0 0 0 0 0]
and model bigger than data
x = [0 1 2 3 4 5 6 7 8 9]
0*x = [0 0 0 0 0]
0'*y = [0 0 0 0 0 0 0 0 0 0]
Note that this operator can be useful in many real-life applications when for example we want to manipulate a subset of the model array and keep intact the rest of the array. For example:
\[\begin{split}\begin{bmatrix} \mathbf{A} \quad \mathbf{0} \end{bmatrix} \begin{bmatrix} \mathbf{x_1} \\ \mathbf{x_2} \end{bmatrix} = \mathbf{A} \mathbf{x_1}\end{split}\]
Refer to the tutorial on Optimization for more details on this.
Total running time of the script: (0 minutes 0.256 seconds)