Slope estimation via Structure Tensor algorithm

This example shows how to estimate local slopes or local dips of a two-dimensional array using pylops.utils.signalprocessing.slope_estimate and pylops.utils.signalprocessing.dip_estimate.

Knowing the local slopes of an image (or a seismic data) can be useful for a variety of tasks in image (or geophysical) processing such as denoising, smoothing, or interpolation. When slopes are used with the pylops.signalprocessing.Seislet operator, the input dataset can be compressed and the sparse nature of the Seislet transform can also be used to precondition sparsity-promoting inverse problems.

We will show examples of a variety of different settings, including a comparison with the original implementation in [1].

1

van Vliet, L. J., Verbeek, P. W., “Estimators for orientation and anisotropy in digitized images”, Journal ASCI Imaging Workshop. 1995.

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.image import imread
from matplotlib.ticker import FuncFormatter, MultipleLocator
from mpl_toolkits.axes_grid1 import make_axes_locatable

import pylops
from pylops.signalprocessing.seislet import _predict_trace
from pylops.utils.signalprocessing import dip_estimate, slope_estimate

plt.close("all")
np.random.seed(10)

Python logo

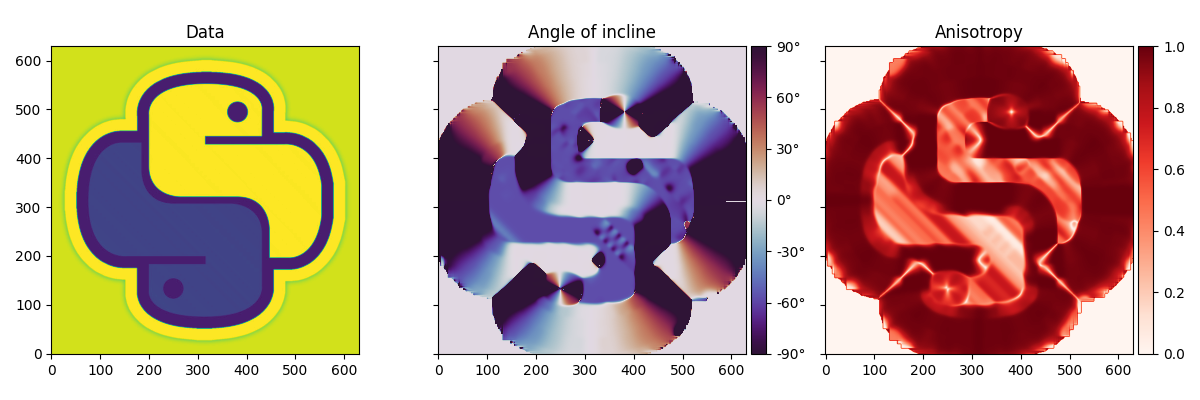
To start we import a 2d image and estimate the local dips of the image.

im = np.load("../testdata/python.npy")[..., 0]
im = im / 255.0 - 0.5

angles, anisotropy = dip_estimate(im, smooth=7)
angles = -np.rad2deg(angles)

fig, axs = plt.subplots(1, 3, figsize=(12, 4), sharex=True, sharey=True)
iax = axs[0].imshow(im, cmap="viridis", origin="lower")
axs[0].set_title("Data")
cax = make_axes_locatable(axs[0]).append_axes("right", size="5%", pad=0.05)
cax.axis("off")

iax = axs[1].imshow(angles, cmap="twilight_shifted", origin="lower", vmin=-90, vmax=90)
axs[1].set_title("Angle of incline")
cax = make_axes_locatable(axs[1]).append_axes("right", size="5%", pad=0.05)
cb = fig.colorbar(
    iax,
    ticks=MultipleLocator(30),
    format=FuncFormatter(lambda x, pos: "{:.0f}°".format(x)),
    cax=cax,
    orientation="vertical",
)

iax = axs[2].imshow(anisotropy, cmap="Reds", origin="lower", vmin=0, vmax=1)
axs[2].set_title("Anisotropy")
cax = make_axes_locatable(axs[2]).append_axes("right", size="5%", pad=0.05)
cb = fig.colorbar(iax, cax=cax, orientation="vertical")
fig.tight_layout()

Seismic data

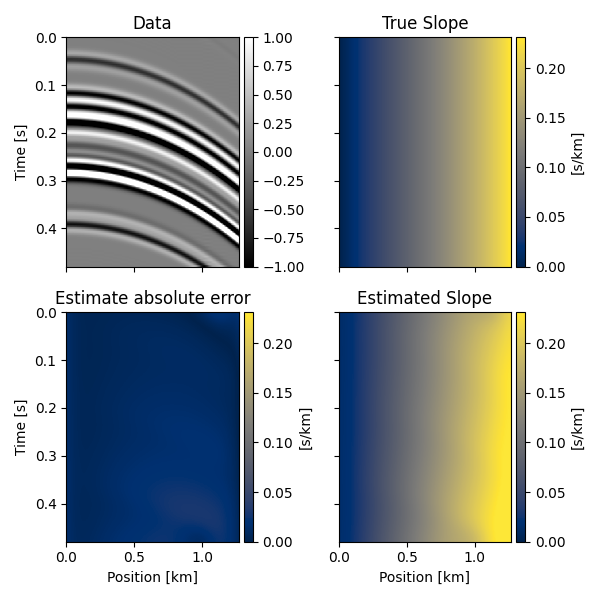
We can now repeat the same using some seismic data. We will first define a single trace and a slope field, apply such slope field to the trace recursively to create the other traces of the data and finally try to recover the underlying slope field from the data alone.

# Reflectivity model
nx, nt = 2**7, 121
dx, dt = 0.01, 0.004
x, t = np.arange(nx) * dx, np.arange(nt) * dt

nspike = nt // 8
refl = np.zeros(nt)
it = np.sort(np.random.permutation(range(10, nt - 20))[:nspike])
refl[it] = np.random.normal(0.0, 1.0, nspike)

# Wavelet
ntwav = 41
f0 = 30
twav = np.arange(ntwav) * dt
wav, *_ = pylops.utils.wavelets.ricker(twav, f0)

# Input trace
trace = np.convolve(refl, wav, mode="same")

# Slopes
theta = np.deg2rad(np.linspace(0, 30, nx))
slope = np.outer(np.ones(nt), np.tan(theta) * dt / dx)

# Model data
d = np.zeros((nt, nx))
tr = trace.copy()
for ix in range(nx):
    tr = _predict_trace(tr, t, dt, dx, slope[:, ix])
    d[:, ix] = tr

# Estimate slopes
slope_est, _ = slope_estimate(d, dt, dx, smooth=10)
slope_est *= -1

fig, axs = plt.subplots(2, 2, figsize=(6, 6), sharex=True, sharey=True)

opts = dict(aspect="auto", extent=(x[0], x[-1], t[-1], t[0]))
iax = axs[0, 0].imshow(d, cmap="gray", vmin=-1, vmax=1, **opts)
axs[0, 0].set(title="Data", ylabel="Time [s]")
cax = make_axes_locatable(axs[0, 0]).append_axes("right", size="5%", pad=0.05)
fig.colorbar(iax, cax=cax, orientation="vertical")

opts.update(dict(cmap="cividis", vmin=np.min(slope), vmax=np.max(slope)))
iax = axs[0, 1].imshow(slope, **opts)
axs[0, 1].set(title="True Slope")
cax = make_axes_locatable(axs[0, 1]).append_axes("right", size="5%", pad=0.05)
fig.colorbar(iax, cax=cax, orientation="vertical")
cax.set_ylabel("[s/km]")

iax = axs[1, 0].imshow(np.abs(slope - slope_est), **opts)
axs[1, 0].set(
    title="Estimate absolute error", ylabel="Time [s]", xlabel="Position [km]"
)
cax = make_axes_locatable(axs[1, 0]).append_axes("right", size="5%", pad=0.05)
fig.colorbar(iax, cax=cax, orientation="vertical")
cax.set_ylabel("[s/km]")

iax = axs[1, 1].imshow(slope_est, **opts)
axs[1, 1].set(title="Estimated Slope", xlabel="Position [km]")
cax = make_axes_locatable(axs[1, 1]).append_axes("right", size="5%", pad=0.05)
fig.colorbar(iax, cax=cax, orientation="vertical")
cax.set_ylabel("[s/km]")

fig.tight_layout()

Concentric circles

The original paper by van Vliet and Verbeek [1] has an example with concentric circles. We recover their original images and compare our implementation with theirs.

def rgb2gray(rgb):
    return np.dot(rgb[..., :3], [0.2989, 0.5870, 0.1140])


circles_input = rgb2gray(imread("../testdata/slope_estimate/concentric.png"))
circles_angles = rgb2gray(imread("../testdata/slope_estimate/concentric_angles.png"))

angles, anisos_sm0 = dip_estimate(circles_input, smooth=0)
angles_sm0 = np.rad2deg(angles)

angles, anisos_sm4 = dip_estimate(circles_input, smooth=4)
angles_sm4 = np.rad2deg(angles)

fig, axs = plt.subplots(2, 3, figsize=(6, 4), sharex=True, sharey=True)
axs[0, 0].imshow(circles_input, cmap="gray", aspect="equal")
axs[0, 0].set(title="Original Image")
cax = make_axes_locatable(axs[0, 0]).append_axes("right", size="5%", pad=0.05)
cax.axis("off")

axs[1, 0].imshow(-circles_angles, cmap="twilight_shifted")
axs[1, 0].set(title="Original Angles")
cax = make_axes_locatable(axs[1, 0]).append_axes("right", size="5%", pad=0.05)
cax.axis("off")

im = axs[0, 1].imshow(angles_sm0, cmap="twilight_shifted", vmin=-90, vmax=90)
cax = make_axes_locatable(axs[0, 1]).append_axes("right", size="5%", pad=0.05)
cb = fig.colorbar(
    im,
    ticks=MultipleLocator(30),
    format=FuncFormatter(lambda x, pos: "{:.0f}°".format(x)),
    cax=cax,
    orientation="vertical",
)
axs[0, 1].set(title="Angles (smooth=0)")

im = axs[1, 1].imshow(angles_sm4, cmap="twilight_shifted", vmin=-90, vmax=90)
cax = make_axes_locatable(axs[1, 1]).append_axes("right", size="5%", pad=0.05)
cb = fig.colorbar(
    im,
    ticks=MultipleLocator(30),
    format=FuncFormatter(lambda x, pos: "{:.0f}°".format(x)),
    cax=cax,
    orientation="vertical",
)
axs[1, 1].set(title="Angles (smooth=4)")

im = axs[0, 2].imshow(anisos_sm0, cmap="Reds", vmin=0, vmax=1)
cax = make_axes_locatable(axs[0, 2]).append_axes("right", size="5%", pad=0.05)
cb = fig.colorbar(im, cax=cax, orientation="vertical")
axs[0, 2].set(title="Anisotropy (smooth=0)")

im = axs[1, 2].imshow(anisos_sm4, cmap="Reds", vmin=0, vmax=1)
cax = make_axes_locatable(axs[1, 2]).append_axes("right", size="5%", pad=0.05)
cb = fig.colorbar(im, cax=cax, orientation="vertical")
axs[1, 2].set(title="Anisotropy (smooth=4)")

for ax in axs.ravel():
    ax.axis("off")
fig.tight_layout()

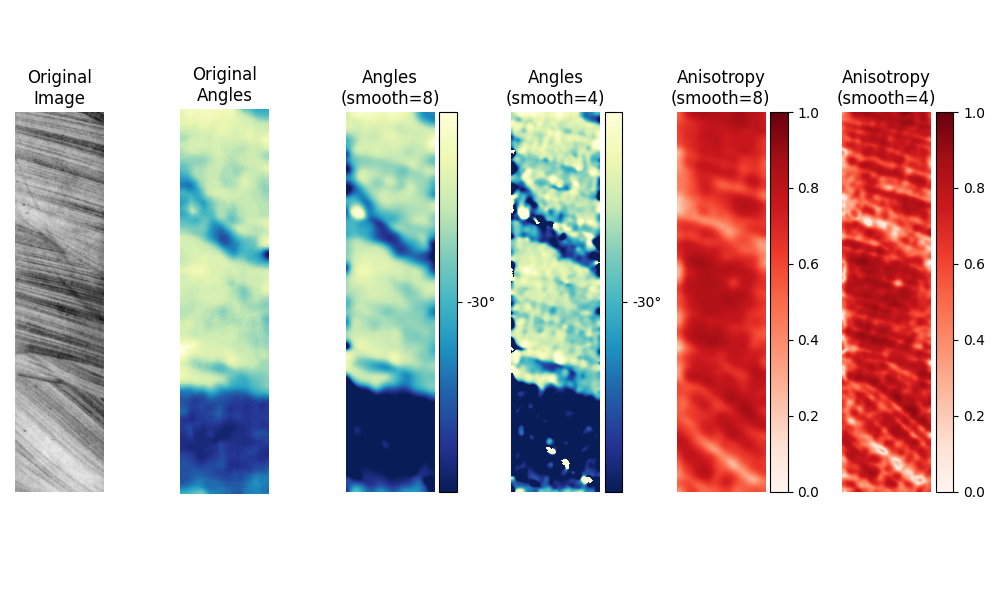
Core samples

The original paper by van Vliet and Verbeek [1] also has an example with images of core samples. Since the original paper does not have a scale with which to plot the angles, we have chosen ours it to match their image as closely as possible.

core_input = rgb2gray(imread("../testdata/slope_estimate/core_sample.png"))
core_angles = rgb2gray(imread("../testdata/slope_estimate/core_sample_orientation.png"))
core_aniso = rgb2gray(imread("../testdata/slope_estimate/core_sample_anisotropy.png"))


angles, anisos_sm4 = dip_estimate(core_input, smooth=4)
angles_sm4 = np.rad2deg(angles)

angles, anisos_sm8 = dip_estimate(core_input, smooth=8)
angles_sm8 = np.rad2deg(angles)

fig, axs = plt.subplots(1, 6, figsize=(10, 6))

axs[0].imshow(core_input, cmap="gray_r", aspect="equal")
axs[0].set(title="Original\nImage")
cax = make_axes_locatable(axs[0]).append_axes("right", size="20%", pad=0.05)
cax.axis("off")

axs[1].imshow(-core_angles, cmap="YlGnBu_r")
axs[1].set(title="Original\nAngles")
cax = make_axes_locatable(axs[1]).append_axes("right", size="20%", pad=0.05)
cax.axis("off")

im = axs[2].imshow(angles_sm8, cmap="YlGnBu_r", vmin=-49, vmax=-11)
cax = make_axes_locatable(axs[2]).append_axes("right", size="20%", pad=0.05)
cb = fig.colorbar(
    im,
    ticks=MultipleLocator(30),
    format=FuncFormatter(lambda x, pos: "{:.0f}°".format(x)),
    cax=cax,
    orientation="vertical",
)
axs[2].set(title="Angles\n(smooth=8)")

im = axs[3].imshow(angles_sm4, cmap="YlGnBu_r", vmin=-49, vmax=-11)
cax = make_axes_locatable(axs[3]).append_axes("right", size="20%", pad=0.05)
cb = fig.colorbar(
    im,
    ticks=MultipleLocator(30),
    format=FuncFormatter(lambda x, pos: "{:.0f}°".format(x)),
    cax=cax,
    orientation="vertical",
)
axs[3].set(title="Angles\n(smooth=4)")

im = axs[4].imshow(anisos_sm8, cmap="Reds", vmin=0, vmax=1)
cax = make_axes_locatable(axs[4]).append_axes("right", size="20%", pad=0.05)
cb = fig.colorbar(im, cax=cax, orientation="vertical")
axs[4].set(title="Anisotropy\n(smooth=8)")

im = axs[5].imshow(anisos_sm4, cmap="Reds", vmin=0, vmax=1)
cax = make_axes_locatable(axs[5]).append_axes("right", size="20%", pad=0.05)
cb = fig.colorbar(im, cax=cax, orientation="vertical")
axs[5].set(title="Anisotropy\n(smooth=4)")

for ax in axs.ravel():
    ax.axis("off")
fig.tight_layout()

Final considerations

As you can see the Structure Tensor algorithm is a very fast, general purpose algorithm that can be used to estimate local slopes to input datasets of very different natures.