Note
Go to the end to download the full example code
Padding#
This example shows how to use the pylops.Pad operator to zero-pad a
model
import matplotlib.pyplot as plt
import numpy as np
import pylops
plt.close("all")
Let’s define a pad operator Pop for one dimensional data
x = [ 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.]
P*x = [ 0. 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 0. 0. 0.]
P'*y = [ 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.]
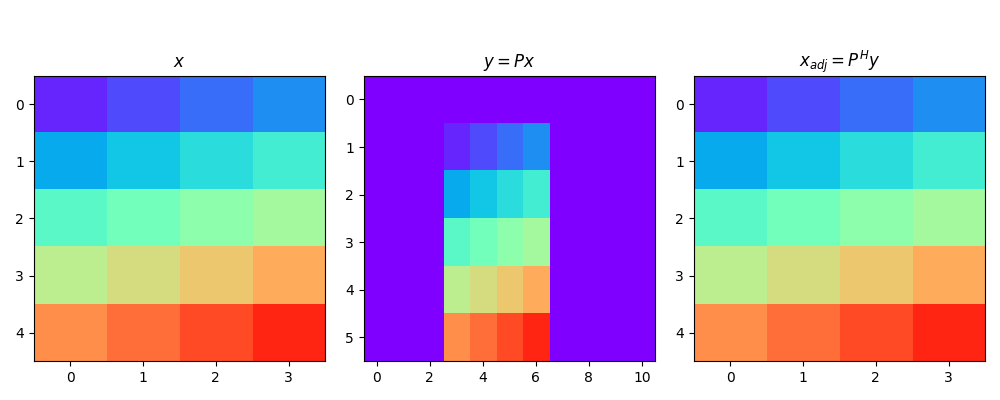
We move now to a multi-dimensional case. We pad the input model with different extents along both dimensions
dims = (5, 4)
pad = ((1, 0), (3, 4))
Pop = pylops.Pad(dims, pad)
x = (np.arange(np.prod(np.array(dims))) + 1.0).reshape(dims)
y = Pop * x
xadj = Pop.H * y
fig, axs = plt.subplots(1, 3, figsize=(10, 4))
fig.suptitle("Pad for 2d data", fontsize=14, fontweight="bold", y=1.15)
axs[0].imshow(x, cmap="rainbow", vmin=0, vmax=np.prod(np.array(dims)) + 1)
axs[0].set_title(r"$x$")
axs[0].axis("tight")
axs[1].imshow(y, cmap="rainbow", vmin=0, vmax=np.prod(np.array(dims)) + 1)
axs[1].set_title(r"$y = P x$")
axs[1].axis("tight")
axs[2].imshow(xadj, cmap="rainbow", vmin=0, vmax=np.prod(np.array(dims)) + 1)
axs[2].set_title(r"$x_{adj} = P^{H} y$")
axs[2].axis("tight")
plt.tight_layout()
Total running time of the script: (0 minutes 0.421 seconds)