pylops.signalprocessing.Convolve2D

pylops.signalprocessing.Convolve2D(dims, h, offset=(0, 0), axes=(-2, -1), method='fft', dtype='float64', name='C')

2D convolution operator.

Apply two-dimensional convolution with a compact filter to model (and data) along a pair of axes of a two or three-dimensional array.

Parameters:

dims : list or int

Number of samples for each dimension

h : numpy.ndarray

2d compact filter to be convolved to input signal

offset : tuple, optional

Indices of the center of the compact filter

axes : int, optional

New in version 2.0.0.

Axes along which convolution is applied

method : str, optional

Method used to calculate the convolution (direct or fft).

dtype : str, optional

Type of elements in input array.

name : str, optional

New in version 2.0.0.

Name of operator (to be used by pylops.utils.describe.describe)

Returns:

cop : pylops.LinearOperator

Convolve2D linear operator

Notes

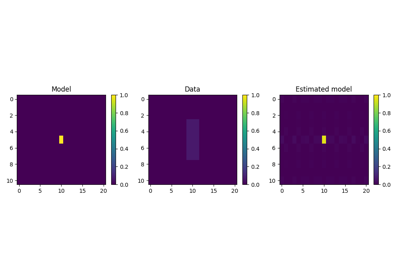
The Convolve2D operator applies two-dimensional convolution between the input signal \(d(t,x)\) and a compact filter kernel \(h(t,x)\) in forward model:

\[y(t,x) = \iint\limits_{-\infty}^{\infty} h(t-\tau,x-\chi) d(\tau,\chi) \,\mathrm{d}\tau \,\mathrm{d}\chi\]

This operation can be discretized as follows

\[y[i,n] = \sum_{j=-\infty}^{\infty} \sum_{m=-\infty}^{\infty} h[i-j,n-m] d[j,m]\]

as well as performed in the frequency domain.

\[Y(f, k_x) = \mathscr{F} (h(t,x)) * \mathscr{F} (d(t,x))\]

Convolve2D operator uses scipy.signal.convolve2d that automatically chooses the best domain for the operation to be carried out.

As the adjoint of convolution is correlation, Convolve2D operator applies correlation in the adjoint mode.

In time domain:

\[y(t,x) = \iint\limits_{-\infty}^{\infty} h(t+\tau,x+\chi) d(\tau,\chi) \,\mathrm{d}\tau \,\mathrm{d}\chi\]

or in frequency domain:

\[y(t, x) = \mathscr{F}^{-1} (H(f, k_x)^* * X(f, k_x))\]

Examples using pylops.signalprocessing.Convolve2D

Convolution

05. Image deblurring