pylops.Diagonal#
- class pylops.Diagonal(diag, dims=None, axis=-1, dtype='float64', name='D')[source]#
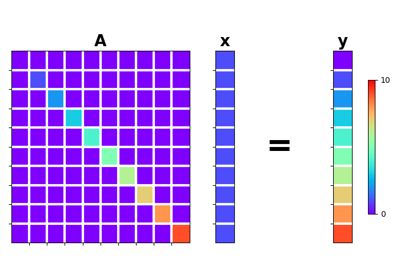
Diagonal operator.
Applies element-wise multiplication of the input vector with the vector
diagin forward and with its complex conjugate in adjoint mode.This operator can also broadcast; in this case the input vector is reshaped into its dimensions
dimsand the element-wise multiplication withdiagis perfomed alongaxis. Note that the vectordiagwill need to have size equal todims[axis].- Parameters
- diag
numpy.ndarray Vector to be used for element-wise multiplication.
- dims
list, optional Number of samples for each dimension (
Noneif only one dimension is available)- axis
int, optional New in version 2.0.0.
Axis along which multiplication is applied.
- dtype
str, optional Type of elements in input array.
- name
str, optional New in version 2.0.0.
Name of operator (to be used by
pylops.utils.describe.describe)
- diag
Notes
Element-wise multiplication between the model \(\mathbf{x}\) and/or data \(\mathbf{y}\) vectors and the array \(\mathbf{d}\) can be expressed as
\[y_i = d_i x_i \quad \forall i=1,2,\ldots,N\]This is equivalent to a matrix-vector multiplication with a matrix containing the vector \(\mathbf{d}\) along its main diagonal.
For real-valued
diag, the Diagonal operator is self-adjoint as the adjoint of a diagonal matrix is the diagonal matrix itself. For complex-valueddiag, the adjoint is equivalent to the element-wise multiplication with the complex conjugate elements ofdiag.- Attributes
Methods
__init__(diag[, dims, axis, dtype, name])adjoint()apply_columns(cols)Apply subset of columns of operator
cond([uselobpcg])Condition number of linear operator.
conj()Complex conjugate operator
div(y[, niter, densesolver])Solve the linear problem \(\mathbf{y}=\mathbf{A}\mathbf{x}\).
dot(x)Matrix-matrix or matrix-vector multiplication.
eigs([neigs, symmetric, niter, uselobpcg])Most significant eigenvalues of linear operator.
matmat(X)Matrix-matrix multiplication.
matrix()Return diagonal matrix as dense
numpy.ndarraymatvec(x)Matrix-vector multiplication.
reset_count()Reset counters
rmatmat(X)Matrix-matrix multiplication.
rmatvec(x)Adjoint matrix-vector multiplication.
todense()Fast implementation of todense based on known structure of the operator
toimag([forw, adj])Imag operator
toreal([forw, adj])Real operator
tosparse()Return sparse matrix.
trace([neval, method, backend])Trace of linear operator.
transpose()