Note
Go to the end to download the full example code
Diagonal#
This example shows how to use the pylops.Diagonal operator
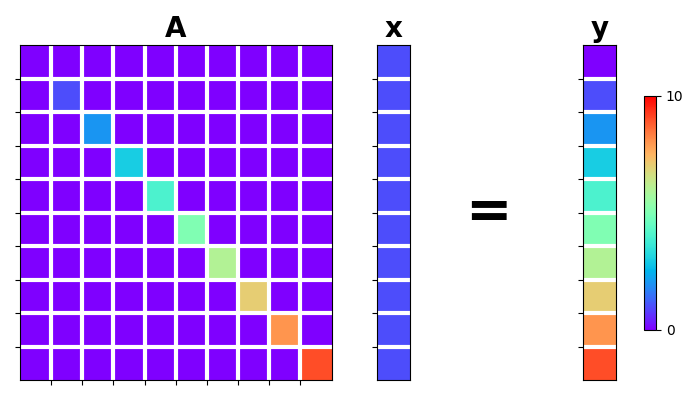
to perform Element-wise multiplication between the input vector and a vector \(\mathbf{d}\).
In other words, the operator acts as a diagonal operator \(\mathbf{D}\) whose elements along the diagonal are the elements of the vector \(\mathbf{d}\).
import matplotlib.gridspec as pltgs
import matplotlib.pyplot as plt
import numpy as np
import pylops
plt.close("all")
Let’s define a diagonal operator \(\mathbf{d}\) with increasing numbers from
0 to N and a unitary model \(\mathbf{x}\).
N = 10
d = np.arange(N)
x = np.ones(N)
Dop = pylops.Diagonal(d)
y = Dop * x
y1 = Dop.H * x
gs = pltgs.GridSpec(1, 6)
fig = plt.figure(figsize=(7, 4))
ax = plt.subplot(gs[0, 0:3])
im = ax.imshow(Dop.matrix(), cmap="rainbow", vmin=0, vmax=N)
ax.set_title("A", size=20, fontweight="bold")
ax.set_xticks(np.arange(N - 1) + 0.5)
ax.set_yticks(np.arange(N - 1) + 0.5)
ax.grid(linewidth=3, color="white")
ax.xaxis.set_ticklabels([])
ax.yaxis.set_ticklabels([])
ax.axis("tight")
ax = plt.subplot(gs[0, 3])
ax.imshow(x[:, np.newaxis], cmap="rainbow", vmin=0, vmax=N)
ax.set_title("x", size=20, fontweight="bold")
ax.set_xticks([])
ax.set_yticks(np.arange(N - 1) + 0.5)
ax.grid(linewidth=3, color="white")
ax.xaxis.set_ticklabels([])
ax.yaxis.set_ticklabels([])
ax = plt.subplot(gs[0, 4])
ax.text(
0.35,
0.5,
"=",
horizontalalignment="center",
verticalalignment="center",
size=40,
fontweight="bold",
)
ax.axis("off")
ax = plt.subplot(gs[0, 5])
ax.imshow(y[:, np.newaxis], cmap="rainbow", vmin=0, vmax=N)
ax.set_title("y", size=20, fontweight="bold")
ax.set_xticks([])
ax.set_yticks(np.arange(N - 1) + 0.5)
ax.grid(linewidth=3, color="white")
ax.xaxis.set_ticklabels([])
ax.yaxis.set_ticklabels([])
fig.colorbar(im, ax=ax, ticks=[0, N], pad=0.3, shrink=0.7)
plt.tight_layout()
Similarly we can consider the input model as composed of two or more dimensions. In this case the diagonal operator can be still applied to each element or broadcasted along a specific direction. Let’s start with the simplest case where each element is multipled by a different value
x =
[[1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1.]]
y = D*x =
[[ 0. 1. 2. 3. 4.]
[ 5. 6. 7. 8. 9.]
[10. 11. 12. 13. 14.]]
xadj = D'*x =
[[ 0. 1. 2. 3. 4.]
[ 5. 6. 7. 8. 9.]
[10. 11. 12. 13. 14.]]
And we now broadcast
nx, ny = 3, 5
x = np.ones((nx, ny))
print(f"x =\n{x}")
# 1st dim
d = np.arange(nx)
Dop = pylops.Diagonal(d, dims=(nx, ny), axis=0)
y = Dop * x.ravel()
y1 = Dop.H * x.ravel()
print(f"1st dim: y = D*x =\n{y.reshape(nx, ny)}")
print(f"1st dim: xadj = D'*x =\n{y1.reshape(nx, ny)}")
# 2nd dim
d = np.arange(ny)
Dop = pylops.Diagonal(d, dims=(nx, ny), axis=1)
y = Dop * x.ravel()
y1 = Dop.H * x.ravel()
print(f"2nd dim: y = D*x =\n{y.reshape(nx, ny)}")
print(f"2nd dim: xadj = D'*x =\n{y1.reshape(nx, ny)}")
x =
[[1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1.]]
1st dim: y = D*x =
[[0. 0. 0. 0. 0.]
[1. 1. 1. 1. 1.]
[2. 2. 2. 2. 2.]]
1st dim: xadj = D'*x =
[[0. 0. 0. 0. 0.]
[1. 1. 1. 1. 1.]
[2. 2. 2. 2. 2.]]
2nd dim: y = D*x =
[[0. 1. 2. 3. 4.]
[0. 1. 2. 3. 4.]
[0. 1. 2. 3. 4.]]
2nd dim: xadj = D'*x =
[[0. 1. 2. 3. 4.]
[0. 1. 2. 3. 4.]
[0. 1. 2. 3. 4.]]
Total running time of the script: (0 minutes 0.320 seconds)
