Wavelet transform

This example shows how to use the pylops.DWT, pylops.DWT2D, and pylops.DWTND operators to perform 1-, 2-, and N-dimensional DWT.

import matplotlib.pyplot as plt
import numpy as np

import pylops

plt.close("all")

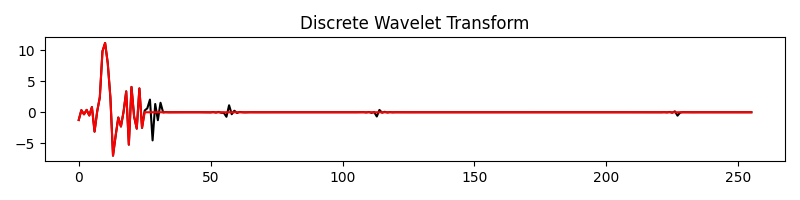
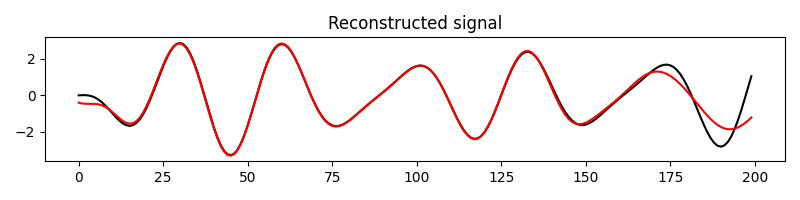
Let’s start with a 1-dimensional signal. We apply the 1-dimensional wavelet transform, keep only the first 30 coefficients and perform the inverse transform.

nt = 200
dt = 0.004
t = np.arange(nt) * dt
freqs = [10, 7, 9]
amps = [1, -2, 0.5]
x = np.sum([amp * np.sin(2 * np.pi * f * t) for (f, amp) in zip(freqs, amps)], axis=0)

Wop = pylops.signalprocessing.DWT(nt, wavelet="dmey", level=5)
y = Wop * x
yf = y.copy()
yf[25:] = 0
xinv = Wop.H * yf

plt.figure(figsize=(8, 2))
plt.plot(y, "k", label="Full")
plt.plot(yf, "r", label="Extracted")
plt.title("Discrete Wavelet Transform")
plt.tight_layout()

plt.figure(figsize=(8, 2))
plt.plot(x, "k", label="Original")
plt.plot(xinv, "r", label="Reconstructed")
plt.title("Reconstructed signal")
plt.tight_layout()

• 
• 

We repeat the same procedure with an image. In this case the 2-dimensional DWT will be applied instead. Only a quarter of the coefficients of the DWT will be retained in this case.

im = np.load("../testdata/python.npy")[::5, ::5, 0]

Nz, Nx = im.shape
Wop = pylops.signalprocessing.DWT2D((Nz, Nx), wavelet="haar", level=5)
y = Wop * im
yf = y.copy()
yf.flat[y.size // 4 :] = 0
iminv = Wop.H * yf

fig, axs = plt.subplots(2, 2, figsize=(6, 6))
axs[0, 0].imshow(im, cmap="gray")
axs[0, 0].set_title("Image")
axs[0, 0].axis("tight")
axs[0, 1].imshow(y, cmap="gray_r", vmin=-1e2, vmax=1e2)
axs[0, 1].set_title("DWT2 coefficients")
axs[0, 1].axis("tight")
axs[1, 0].imshow(iminv, cmap="gray")
axs[1, 0].set_title("Reconstructed image")
axs[1, 0].axis("tight")
axs[1, 1].imshow(yf, cmap="gray_r", vmin=-1e2, vmax=1e2)
axs[1, 1].set_title("DWT2 coefficients (zeroed)")
axs[1, 1].axis("tight")
plt.tight_layout()

Let us now try the same with a 3D volumetric model, where we use the N-dimensional DWT. This time, we only retain 10 percent of the coefficients of the DWT.

nx = 128
ny = 256
nz = 128

x = np.arange(nx)
y = np.arange(ny)
z = np.arange(nz)

xx, yy, zz = np.meshgrid(x, y, z, indexing="ij")
# Generate a 3D model with two block anomalies
m = np.ones_like(xx, dtype=float)
block1 = (xx > 10) & (xx < 60) & (yy > 100) & (yy < 150) & (zz > 20) & (zz < 70)
block2 = (xx > 70) & (xx < 80) & (yy > 100) & (yy < 200) & (zz > 10) & (zz < 50)
m[block1] = 1.2
m[block2] = 0.8
Wop = pylops.signalprocessing.DWTND((nx, ny, nz), wavelet="haar", level=3)
y = Wop * m

ratio = 0.1
yf = y.copy()
yf.flat[int(ratio * y.size) :] = 0
iminv = Wop.H * yf

fig, axs = plt.subplots(2, 2, figsize=(6, 6))
axs[0, 0].imshow(m[:, :, 30], cmap="gray")
axs[0, 0].set_title("Model (Slice at z=30)")
axs[0, 0].axis("tight")
axs[0, 1].imshow(y[:, :, 90], cmap="gray_r")
axs[0, 1].set_title("DWTNT coefficients")
axs[0, 1].axis("tight")
axs[1, 0].imshow(iminv[:, :, 30], cmap="gray")
axs[1, 0].set_title("Reconstructed model (Slice at z=30)")
axs[1, 0].axis("tight")
axs[1, 1].imshow(yf[:, :, 90], cmap="gray_r")
axs[1, 1].set_title("DWTNT coefficients (zeroed)")
axs[1, 1].axis("tight")
plt.tight_layout()