09. Multi-Dimensional Deconvolution

This example shows how to set-up and run the pylops.waveeqprocessing.MDD inversion using synthetic data.

import warnings

import matplotlib.pyplot as plt
import numpy as np

import pylops
from pylops.utils.seismicevents import hyperbolic2d, makeaxis
from pylops.utils.tapers import taper3d
from pylops.utils.wavelets import ricker

warnings.filterwarnings("ignore")
plt.close("all")

# sphinx_gallery_thumbnail_number = 5

Let’s start by creating a set of hyperbolic events to be used as our MDC kernel

# Input parameters
par = {
    "ox": -150,
    "dx": 10,
    "nx": 31,
    "oy": -250,
    "dy": 10,
    "ny": 51,
    "ot": 0,
    "dt": 0.004,
    "nt": 300,
    "f0": 20,
    "nfmax": 200,
}

t0_m = [0.2]
vrms_m = [700.0]
amp_m = [1.0]

t0_G = [0.2, 0.5, 0.7]
vrms_G = [800.0, 1200.0, 1500.0]
amp_G = [1.0, 0.6, 0.5]

# Taper
tap = taper3d(par["nt"], [par["ny"], par["nx"]], (5, 5), tapertype="hanning")

# Create axis
t, t2, x, y = makeaxis(par)

# Create wavelet
wav = ricker(t[:41], f0=par["f0"])[0]

# Generate model
m, mwav = hyperbolic2d(x, t, t0_m, vrms_m, amp_m, wav)

# Generate operator
G, Gwav = np.zeros((par["ny"], par["nx"], par["nt"])), np.zeros(
    (par["ny"], par["nx"], par["nt"])
)
for iy, y0 in enumerate(y):
    G[iy], Gwav[iy] = hyperbolic2d(x - y0, t, t0_G, vrms_G, amp_G, wav)
G, Gwav = G * tap, Gwav * tap

# Add negative part to data and model
m = np.concatenate((np.zeros((par["nx"], par["nt"] - 1)), m), axis=-1)
mwav = np.concatenate((np.zeros((par["nx"], par["nt"] - 1)), mwav), axis=-1)
Gwav2 = np.concatenate((np.zeros((par["ny"], par["nx"], par["nt"] - 1)), Gwav), axis=-1)

# Define MDC linear operator
Gwav_fft = np.fft.rfft(Gwav2, 2 * par["nt"] - 1, axis=-1)
Gwav_fft = (Gwav_fft[..., : par["nfmax"]]).transpose(2, 0, 1)

MDCop = pylops.waveeqprocessing.MDC(
    Gwav_fft,
    nt=2 * par["nt"] - 1,
    nv=1,
    dt=0.004,
    dr=1.0,
)

# Create data
d = MDCop * m.T.ravel()
d = d.reshape(2 * par["nt"] - 1, par["ny"]).T

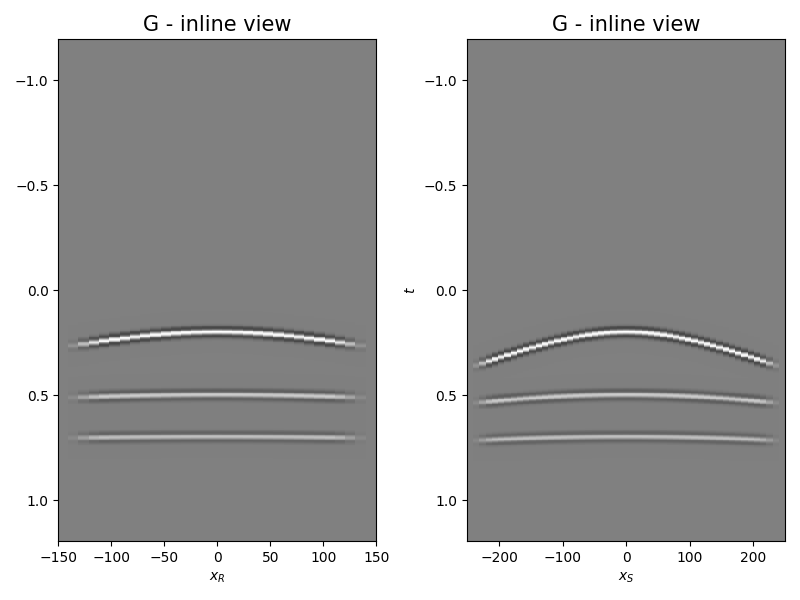
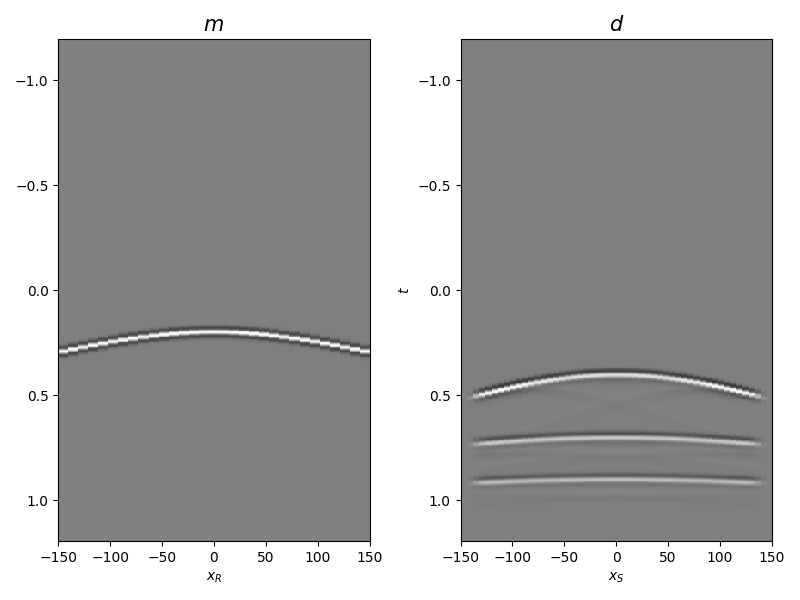
Let’s display what we have so far: operator, input model, and data

fig, axs = plt.subplots(1, 2, figsize=(8, 6))
axs[0].imshow(
    Gwav2[int(par["ny"] / 2)].T,
    aspect="auto",
    interpolation="nearest",
    cmap="gray",
    vmin=-np.abs(Gwav2.max()),
    vmax=np.abs(Gwav2.max()),
    extent=(x.min(), x.max(), t2.max(), t2.min()),
)
axs[0].set_title("G - inline view", fontsize=15)
axs[0].set_xlabel(r"$x_R$")
axs[1].set_ylabel(r"$t$")
axs[1].imshow(
    Gwav2[:, int(par["nx"] / 2)].T,
    aspect="auto",
    interpolation="nearest",
    cmap="gray",
    vmin=-np.abs(Gwav2.max()),
    vmax=np.abs(Gwav2.max()),
    extent=(y.min(), y.max(), t2.max(), t2.min()),
)
axs[1].set_title("G - inline view", fontsize=15)
axs[1].set_xlabel(r"$x_S$")
axs[1].set_ylabel(r"$t$")
fig.tight_layout()

fig, axs = plt.subplots(1, 2, figsize=(8, 6))
axs[0].imshow(
    mwav.T,
    aspect="auto",
    interpolation="nearest",
    cmap="gray",
    vmin=-np.abs(mwav.max()),
    vmax=np.abs(mwav.max()),
    extent=(x.min(), x.max(), t2.max(), t2.min()),
)
axs[0].set_title(r"$m$", fontsize=15)
axs[0].set_xlabel(r"$x_R$")
axs[1].set_ylabel(r"$t$")
axs[1].imshow(
    d.T,
    aspect="auto",
    interpolation="nearest",
    cmap="gray",
    vmin=-np.abs(d.max()),
    vmax=np.abs(d.max()),
    extent=(x.min(), x.max(), t2.max(), t2.min()),
)
axs[1].set_title(r"$d$", fontsize=15)
axs[1].set_xlabel(r"$x_S$")
axs[1].set_ylabel(r"$t$")
fig.tight_layout()

• 
• 

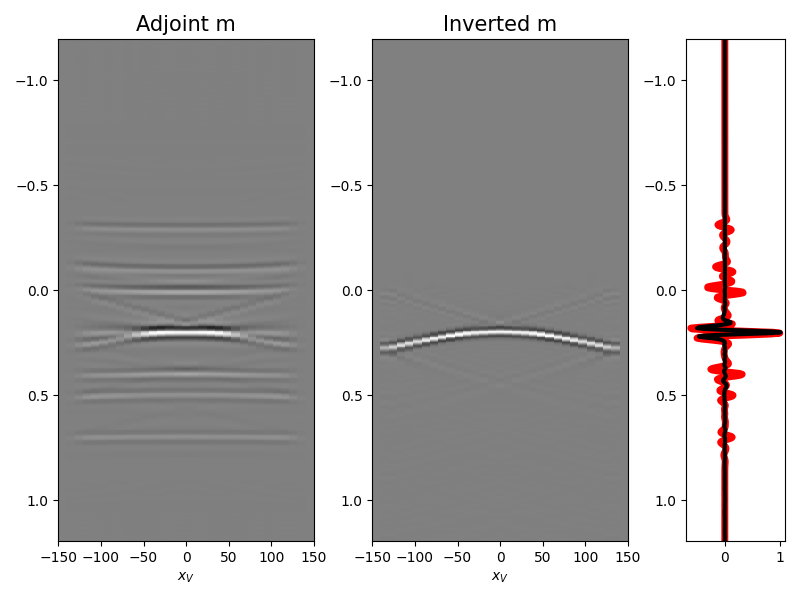
We are now ready to feed our operator to pylops.waveeqprocessing.MDD and invert back for our input model

minv, madj, psfinv, psfadj = pylops.waveeqprocessing.MDD(
    Gwav,
    d[:, par["nt"] - 1 :],
    dt=par["dt"],
    dr=par["dx"],
    nfmax=par["nfmax"],
    wav=wav,
    twosided=True,
    add_negative=True,
    adjoint=True,
    psf=True,
    dottest=False,
    **dict(damp=1e-4, iter_lim=20, show=0)
)

fig = plt.figure(figsize=(8, 6))
ax1 = plt.subplot2grid((1, 5), (0, 0), colspan=2)
ax2 = plt.subplot2grid((1, 5), (0, 2), colspan=2)
ax3 = plt.subplot2grid((1, 5), (0, 4))
ax1.imshow(
    madj.T,
    aspect="auto",
    interpolation="nearest",
    cmap="gray",
    vmin=-np.abs(madj.max()),
    vmax=np.abs(madj.max()),
    extent=(x.min(), x.max(), t2.max(), t2.min()),
)
ax1.set_title("Adjoint m", fontsize=15)
ax1.set_xlabel(r"$x_V$")
axs[1].set_ylabel(r"$t$")
ax2.imshow(
    minv.T,
    aspect="auto",
    interpolation="nearest",
    cmap="gray",
    vmin=-np.abs(minv.max()),
    vmax=np.abs(minv.max()),
    extent=(x.min(), x.max(), t2.max(), t2.min()),
)
ax2.set_title("Inverted m", fontsize=15)
ax2.set_xlabel(r"$x_V$")
axs[1].set_ylabel(r"$t$")
ax3.plot(
    madj[int(par["nx"] / 2)] / np.abs(madj[int(par["nx"] / 2)]).max(), t2, "r", lw=5
)
ax3.plot(
    minv[int(par["nx"] / 2)] / np.abs(minv[int(par["nx"] / 2)]).max(), t2, "k", lw=3
)
ax3.set_ylim([t2[-1], t2[0]])
fig.tight_layout()

fig, axs = plt.subplots(1, 2, figsize=(8, 6))
axs[0].imshow(
    psfinv[int(par["nx"] / 2)].T,
    aspect="auto",
    interpolation="nearest",
    vmin=-np.abs(psfinv.max()),
    vmax=np.abs(psfinv.max()),
    cmap="gray",
    extent=(x.min(), x.max(), t2.max(), t2.min()),
)
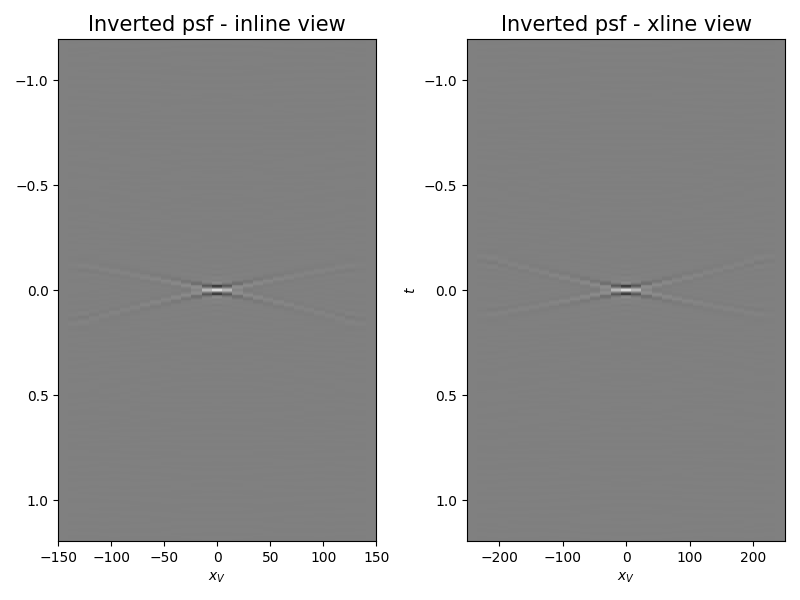
axs[0].set_title("Inverted psf - inline view", fontsize=15)
axs[0].set_xlabel(r"$x_V$")
axs[1].set_ylabel(r"$t$")
axs[1].imshow(
    psfinv[:, int(par["nx"] / 2)].T,
    aspect="auto",
    interpolation="nearest",
    vmin=-np.abs(psfinv.max()),
    vmax=np.abs(psfinv.max()),
    cmap="gray",
    extent=(y.min(), y.max(), t2.max(), t2.min()),
)
axs[1].set_title("Inverted psf - xline view", fontsize=15)
axs[1].set_xlabel(r"$x_V$")
axs[1].set_ylabel(r"$t$")
fig.tight_layout()

• 
• 

We repeat the same procedure but this time we will add a preconditioning by means of causality_precond parameter, which enforces the inverted model to be zero in the negative part of the time axis (as expected by theory). This preconditioning will have the effect of speeding up the convergence of the iterative solver and thus reduce the computation time of the deconvolution

minvprec = pylops.waveeqprocessing.MDD(
    Gwav,
    d[:, par["nt"] - 1 :],
    dt=par["dt"],
    dr=par["dx"],
    nfmax=par["nfmax"],
    wav=wav,
    twosided=True,
    add_negative=True,
    adjoint=False,
    psf=False,
    causality_precond=True,
    dottest=False,
    **dict(damp=1e-4, iter_lim=50, show=0)
)

fig = plt.figure(figsize=(8, 6))
ax1 = plt.subplot2grid((1, 5), (0, 0), colspan=2)
ax2 = plt.subplot2grid((1, 5), (0, 2), colspan=2)
ax3 = plt.subplot2grid((1, 5), (0, 4))
ax1.imshow(
    madj.T,
    aspect="auto",
    interpolation="nearest",
    cmap="gray",
    vmin=-np.abs(madj.max()),
    vmax=np.abs(madj.max()),
    extent=(x.min(), x.max(), t2.max(), t2.min()),
)
ax1.set_title("Adjoint m", fontsize=15)
ax1.set_xlabel(r"$x_V$")
axs[1].set_ylabel(r"$t$")
ax2.imshow(
    minvprec.T,
    aspect="auto",
    interpolation="nearest",
    cmap="gray",
    vmin=-np.abs(minvprec.max()),
    vmax=np.abs(minvprec.max()),
    extent=(x.min(), x.max(), t2.max(), t2.min()),
)
ax2.set_title("Inverted m", fontsize=15)
ax2.set_xlabel(r"$x_V$")
axs[1].set_ylabel(r"$t$")
ax3.plot(
    madj[int(par["nx"] / 2)] / np.abs(madj[int(par["nx"] / 2)]).max(), t2, "r", lw=5
)
ax3.plot(
    minvprec[int(par["nx"] / 2)] / np.abs(minv[int(par["nx"] / 2)]).max(), t2, "k", lw=3
)
ax3.set_ylim([t2[-1], t2[0]])
fig.tight_layout()