pylops.Smoothing2D#
- class pylops.Smoothing2D(nsmooth, dims, axes=(-2, -1), dtype='float64', name='S')[source]#
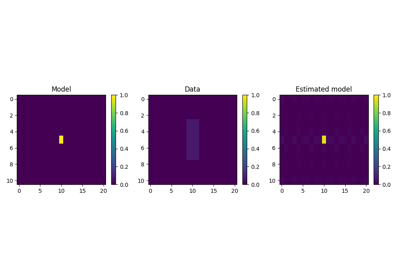
2D Smoothing.
Apply smoothing to model (and data) along two
axesof a multi-dimensional array.- Parameters
See also
pylops.signalprocessing.Convolve2D2D convolution
Notes
The 2D Smoothing operator is a special type of convolutional operator that convolves the input model (or data) with a constant 2d filter of size \(n_{\text{smooth}, 1} \times n_{\text{smooth}, 2}\):
Its application to a two dimensional input signal is:
\[y[i,j] = 1/(n_{\text{smooth}, 1}\cdot n_{\text{smooth}, 2}) \sum_{l=-(n_{\text{smooth},1}-1)/2}^{(n_{\text{smooth},1}-1)/2} \sum_{m=-(n_{\text{smooth},2}-1)/2}^{(n_{\text{smooth},2}-1)/2} x[l,m]\]Note that since the filter is symmetrical, the Smoothing2D operator is self-adjoint.
- Attributes
Methods
__init__(nsmooth, dims[, axes, dtype, name])adjoint()apply_columns(cols)Apply subset of columns of operator
cond([uselobpcg])Condition number of linear operator.
conj()Complex conjugate operator
div(y[, niter, densesolver])Solve the linear problem \(\mathbf{y}=\mathbf{A}\mathbf{x}\).
dot(x)Matrix-matrix or matrix-vector multiplication.
eigs([neigs, symmetric, niter, uselobpcg])Most significant eigenvalues of linear operator.
matmat(X)Matrix-matrix multiplication.
matvec(x)Matrix-vector multiplication.
reset_count()Reset counters
rmatmat(X)Matrix-matrix multiplication.
rmatvec(x)Adjoint matrix-vector multiplication.
todense([backend])Return dense matrix.
toimag([forw, adj])Imag operator
toreal([forw, adj])Real operator
tosparse()Return sparse matrix.
trace([neval, method, backend])Trace of linear operator.
transpose()