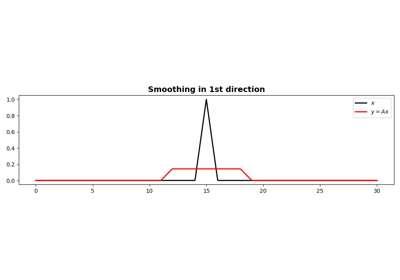
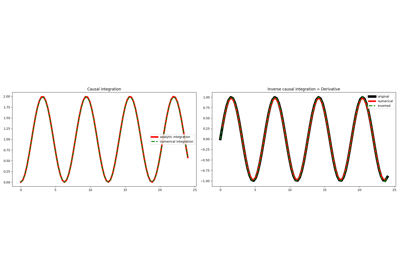
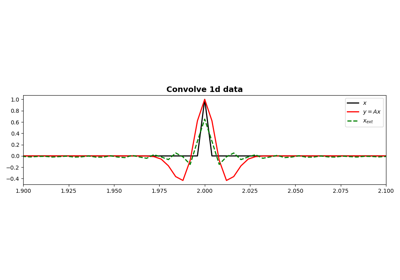
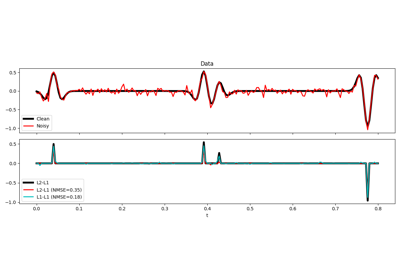
pylops.signalprocessing.Convolve1D#

class pylops.signalprocessing.Convolve1D(dims, h, offset=0, axis=-1, method=None, dtype='float64', name='C')[source]#

1D convolution operator.

Apply one-dimensional convolution with a compact filter to model (and data) along an axis of a multi-dimensional array.

Parameters

dimslist or int: Number of samples for each dimension
hnumpy.ndarray: 1d compact filter to be convolved to input signal
offsetint: Index of the center of the compact filter
axisint, optional: New in version 2.0.0.

Axis along which convolution is applied
methodstr, optional: Method used to calculate the convolution (direct, fft, or overlapadd). Note that only direct and fft are allowed when dims=None, whilst fft and overlapadd are allowed when dims is provided.
dtypestr, optional: Type of elements in input array.
namestr, optional: New in version 2.0.0.

Name of operator (to be used by pylops.utils.describe.describe)

Raises

ValueError: If offset is bigger than len(h) - 1
NotImplementedError: If method provided is not allowed

Notes

The Convolve1D operator applies convolution between the input signal \(x(t)\) and a compact filter kernel \(h(t)\) in forward model:

\[y(t) = \int\limits_{-\infty}^{\infty} h(t-\tau) x(\tau) \,\mathrm{d}\tau\]

This operation can be discretized as follows

\[y[n] = \sum_{m=-\infty}^{\infty} h[n-m] x[m]\]

as well as performed in the frequency domain.

\[Y(f) = \mathscr{F} (h(t)) * \mathscr{F} (x(t))\]

Convolve1D operator uses scipy.signal.convolve that automatically chooses the best domain for the operation to be carried out for one dimensional inputs. The fft implementation scipy.signal.fftconvolve is however enforced for signals in 2 or more dimensions as this routine efficently operates on multi-dimensional arrays.

As the adjoint of convolution is correlation, Convolve1D operator applies correlation in the adjoint mode.

In time domain:

\[x(t) = \int\limits_{-\infty}^{\infty} h(t+\tau) x(\tau) \,\mathrm{d}\tau\]

or in frequency domain:

\[y(t) = \mathscr{F}^{-1} (H(f)^* * X(f))\]

Attributes

shapetuple: Operator shape
explicitbool: Operator contains a matrix that can be solved explicitly (True) or not (False)

Methods

`__init__`(dims, h[, offset, axis, method, ...])
`adjoint`()
`apply_columns`(cols)	Apply subset of columns of operator
`cond`([uselobpcg])	Condition number of linear operator.
`conj`()	Complex conjugate operator
`div`(y[, niter, densesolver])	Solve the linear problem \(\mathbf{y}=\mathbf{A}\mathbf{x}\).
`dot`(x)	Matrix-matrix or matrix-vector multiplication.
`eigs`([neigs, symmetric, niter, uselobpcg])	Most significant eigenvalues of linear operator.
`matmat`(X)	Matrix-matrix multiplication.
`matvec`(x)	Matrix-vector multiplication.
`reset_count`()	Reset counters
`rmatmat`(X)	Matrix-matrix multiplication.
`rmatvec`(x)	Adjoint matrix-vector multiplication.
`todense`([backend])	Return dense matrix.
`toimag`([forw, adj])	Imag operator
`toreal`([forw, adj])	Real operator
`tosparse`()	Return sparse matrix.
`trace`([neval, method, backend])	Trace of linear operator.
`transpose`()