Note
Go to the end to download the full example code
15. Least-squares migration#
Seismic migration is the process by which seismic data are manipulated to create an image of the subsurface reflectivity.
While traditionally solved as the adjont of the demigration operator, it is becoming more and more common to solve the underlying inverse problem in the quest for more accurate and detailed subsurface images.
Indipendently of the choice of the modelling operator (i.e., ray-based or full wavefield-based), the demigration/migration process can be expressed as a linear operator of such a kind:
where \(m(\mathbf{x})\) is the reflectivity at every location in the subsurface, \(G(\mathbf{x}, \mathbf{x_s}, t)\) and \(G(\mathbf{x_r}, \mathbf{x}, t)\) are the Green’s functions from source-to-subsurface-to-receiver and finally \(w(t)\) is the wavelet. Ultimately, while the Green’s functions can be computed in many different ways, solving this system of equations for the reflectivity model is what we generally refer to as Least-squares migration (LSM).
In this tutorial we will consider the most simple scenario where we use an
eikonal solver to compute the Green’s functions and show how we can use the
pylops.waveeqprocessing.LSM operator to perform LSM.
import matplotlib.pyplot as plt
import numpy as np
from scipy.sparse.linalg import lsqr
import pylops
plt.close("all")
np.random.seed(0)
To start we create a simple model with 2 interfaces
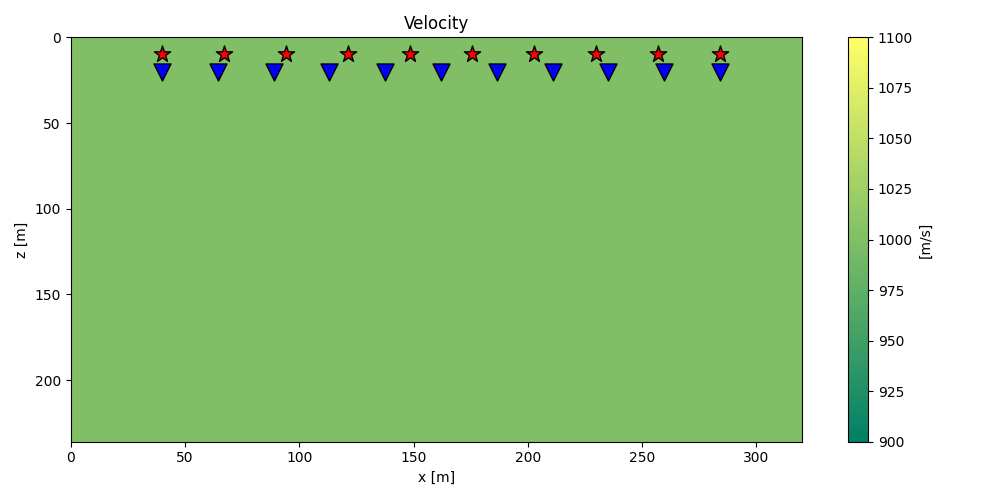
# Velocity Model
nx, nz = 81, 60
dx, dz = 4, 4
x, z = np.arange(nx) * dx, np.arange(nz) * dz
v0 = 1000 # initial velocity
kv = 0.0 # gradient
vel = np.outer(np.ones(nx), v0 + kv * z)
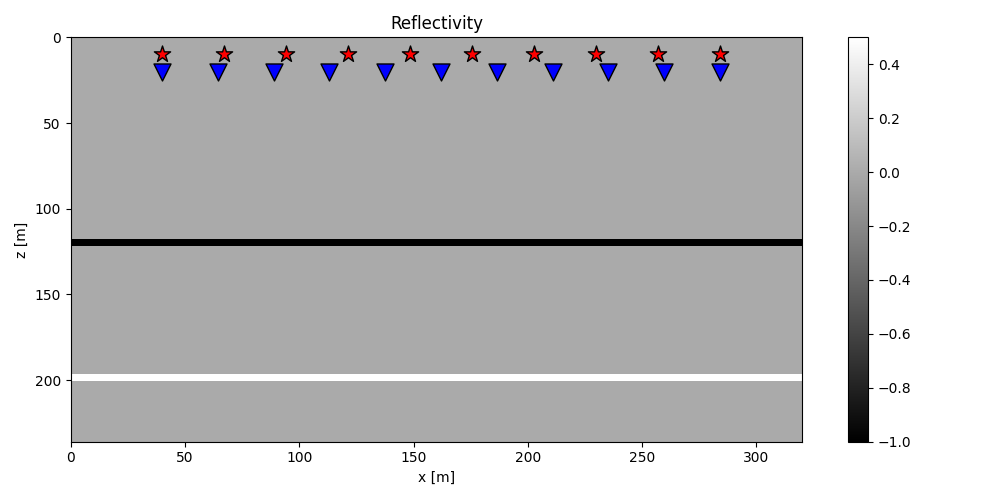
# Reflectivity Model
refl = np.zeros((nx, nz))
refl[:, 30] = -1
refl[:, 50] = 0.5
# Receivers
nr = 11
rx = np.linspace(10 * dx, (nx - 10) * dx, nr)
rz = 20 * np.ones(nr)
recs = np.vstack((rx, rz))
dr = recs[0, 1] - recs[0, 0]
# Sources
ns = 10
sx = np.linspace(dx * 10, (nx - 10) * dx, ns)
sz = 10 * np.ones(ns)
sources = np.vstack((sx, sz))
ds = sources[0, 1] - sources[0, 0]
plt.figure(figsize=(10, 5))
im = plt.imshow(vel.T, cmap="summer", extent=(x[0], x[-1], z[-1], z[0]))
plt.scatter(recs[0], recs[1], marker="v", s=150, c="b", edgecolors="k")
plt.scatter(sources[0], sources[1], marker="*", s=150, c="r", edgecolors="k")
cb = plt.colorbar(im)
cb.set_label("[m/s]")
plt.axis("tight")
plt.xlabel("x [m]"), plt.ylabel("z [m]")
plt.title("Velocity")
plt.xlim(x[0], x[-1])
plt.tight_layout()
plt.figure(figsize=(10, 5))
im = plt.imshow(refl.T, cmap="gray", extent=(x[0], x[-1], z[-1], z[0]))
plt.scatter(recs[0], recs[1], marker="v", s=150, c="b", edgecolors="k")
plt.scatter(sources[0], sources[1], marker="*", s=150, c="r", edgecolors="k")
plt.colorbar(im)
plt.axis("tight")
plt.xlabel("x [m]"), plt.ylabel("z [m]")
plt.title("Reflectivity")
plt.xlim(x[0], x[-1])
plt.tight_layout()
We can now create our LSM object and invert for the reflectivity using two
different solvers: scipy.sparse.linalg.lsqr (LS solution) and
pylops.optimization.sparsity.fista (LS solution with sparse model).
nt = 651
dt = 0.004
t = np.arange(nt) * dt
wav, wavt, wavc = pylops.utils.wavelets.ricker(t[:41], f0=20)
lsm = pylops.waveeqprocessing.LSM(
z,
x,
t,
sources,
recs,
v0,
wav,
wavc,
mode="analytic",
engine="numba",
)
d = lsm.Demop * refl
madj = lsm.Demop.H * d
minv = lsm.solve(d.ravel(), solver=lsqr, **dict(iter_lim=100))
minv = minv.reshape(nx, nz)
minv_sparse = lsm.solve(
d.ravel(), solver=pylops.optimization.sparsity.fista, **dict(eps=1e2, niter=100)
)
minv_sparse = minv_sparse.reshape(nx, nz)
# demigration
d = d.reshape(ns, nr, nt)
dadj = lsm.Demop * madj # (ns * nr, nt)
dadj = dadj.reshape(ns, nr, nt)
dinv = lsm.Demop * minv
dinv = dinv.reshape(ns, nr, nt)
dinv_sparse = lsm.Demop * minv_sparse
dinv_sparse = dinv_sparse.reshape(ns, nr, nt)
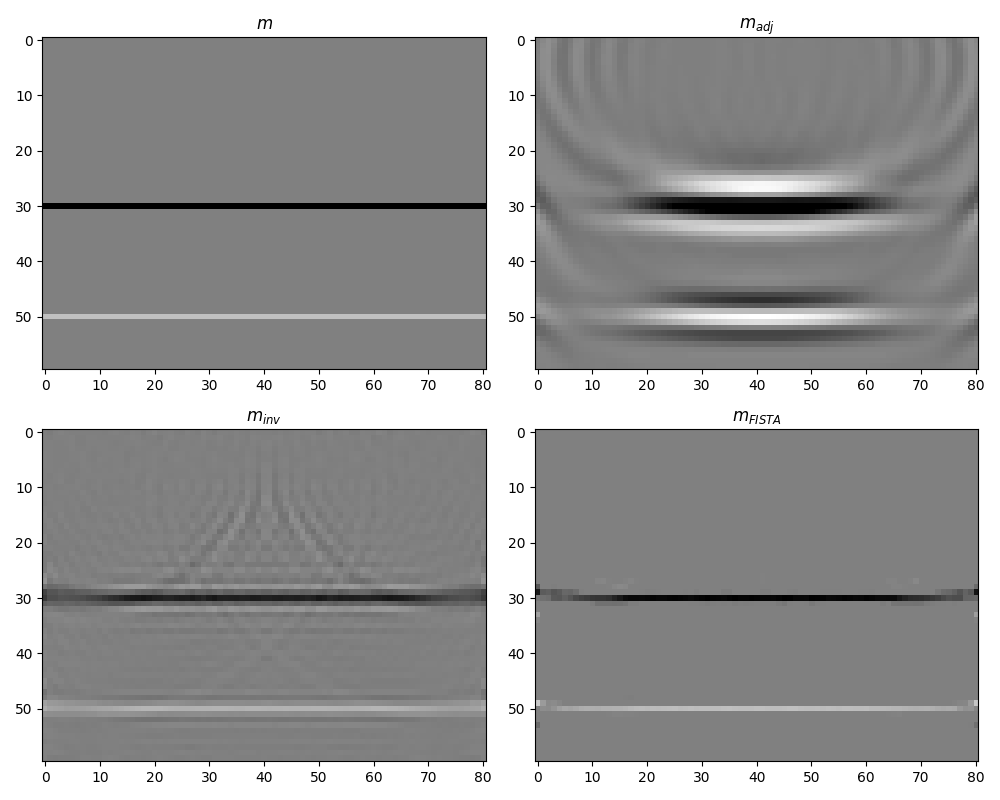
# sphinx_gallery_thumbnail_number = 2
fig, axs = plt.subplots(2, 2, figsize=(10, 8))
axs[0][0].imshow(refl.T, cmap="gray", vmin=-1, vmax=1)
axs[0][0].axis("tight")
axs[0][0].set_title(r"$m$")
axs[0][1].imshow(madj.T, cmap="gray", vmin=-madj.max(), vmax=madj.max())
axs[0][1].set_title(r"$m_{adj}$")
axs[0][1].axis("tight")
axs[1][0].imshow(minv.T, cmap="gray", vmin=-1, vmax=1)
axs[1][0].axis("tight")
axs[1][0].set_title(r"$m_{inv}$")
axs[1][1].imshow(minv_sparse.T, cmap="gray", vmin=-1, vmax=1)
axs[1][1].axis("tight")
axs[1][1].set_title(r"$m_{FISTA}$")
plt.tight_layout()
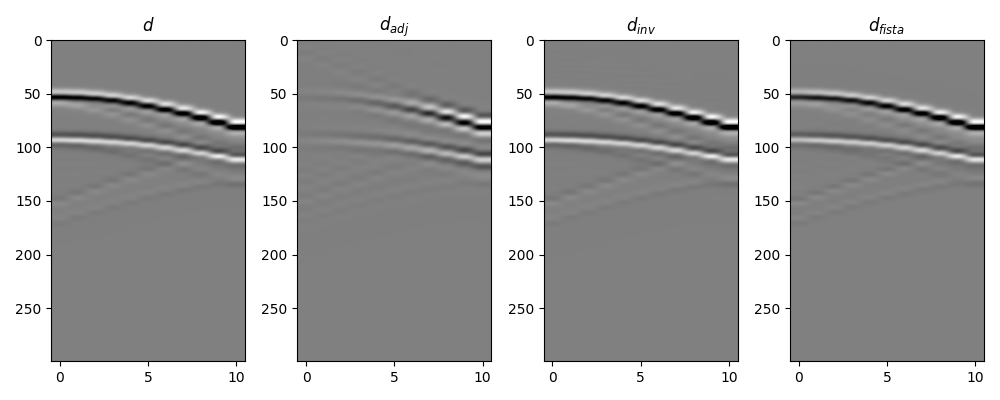
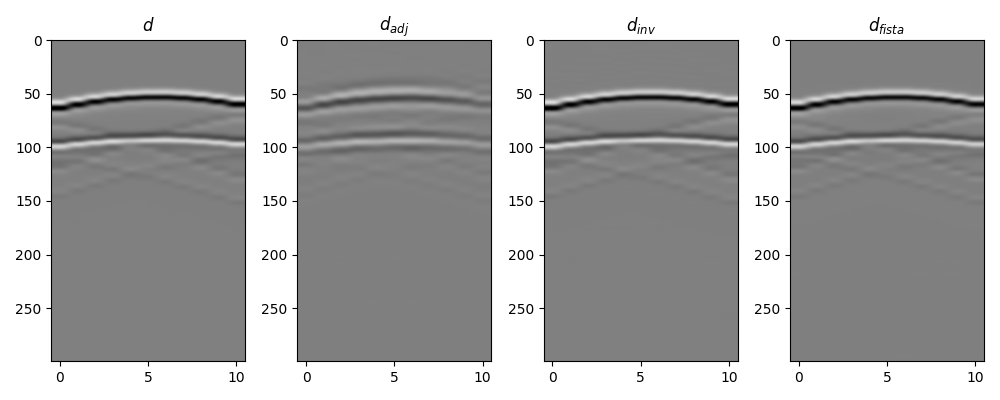
fig, axs = plt.subplots(1, 4, figsize=(10, 4))
axs[0].imshow(d[0, :, :300].T, cmap="gray", vmin=-d.max(), vmax=d.max())
axs[0].set_title(r"$d$")
axs[0].axis("tight")
axs[1].imshow(dadj[0, :, :300].T, cmap="gray", vmin=-dadj.max(), vmax=dadj.max())
axs[1].set_title(r"$d_{adj}$")
axs[1].axis("tight")
axs[2].imshow(dinv[0, :, :300].T, cmap="gray", vmin=-d.max(), vmax=d.max())
axs[2].set_title(r"$d_{inv}$")
axs[2].axis("tight")
axs[3].imshow(dinv_sparse[0, :, :300].T, cmap="gray", vmin=-d.max(), vmax=d.max())
axs[3].set_title(r"$d_{fista}$")
axs[3].axis("tight")
plt.tight_layout()
fig, axs = plt.subplots(1, 4, figsize=(10, 4))
axs[0].imshow(d[ns // 2, :, :300].T, cmap="gray", vmin=-d.max(), vmax=d.max())
axs[0].set_title(r"$d$")
axs[0].axis("tight")
axs[1].imshow(dadj[ns // 2, :, :300].T, cmap="gray", vmin=-dadj.max(), vmax=dadj.max())
axs[1].set_title(r"$d_{adj}$")
axs[1].axis("tight")
axs[2].imshow(dinv[ns // 2, :, :300].T, cmap="gray", vmin=-d.max(), vmax=d.max())
axs[2].set_title(r"$d_{inv}$")
axs[2].axis("tight")
axs[3].imshow(dinv_sparse[ns // 2, :, :300].T, cmap="gray", vmin=-d.max(), vmax=d.max())
axs[3].set_title(r"$d_{fista}$")
axs[3].axis("tight")
plt.tight_layout()
This was just a short teaser, for a more advanced set of examples of 2D and 3D traveltime-based LSM head over to this notebook.
Total running time of the script: (0 minutes 7.011 seconds)