pylops.Pad

class pylops.Pad(dims, pad, dtype='float64', name='P')

Pad operator.

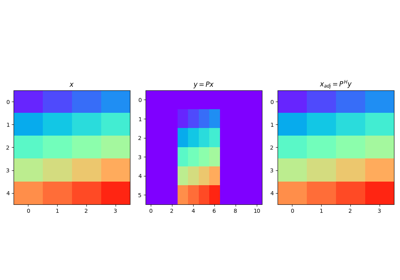
Zero-pad model in forward model and extract non-zero subsequence in adjoint. Padding can be performed in one or multiple directions to any multi-dimensional input arrays.

Parameters

dimsint or tuple

Number of samples for each dimension

padtuple

Number of samples to pad. If dims is a scalar, pad is a single tuple (pad_in, pad_end). If dims is a tuple, pad is a tuple of tuples where each inner tuple contains the number of samples to pad in each dimension

dtypestr, optional

Type of elements in input array.

namestr, optional

New in version 2.0.0.

Name of operator (to be used by pylops.utils.describe.describe)

Raises

ValueError

If any element of pad is negative.

Notes

Given an array of size \(N\), the Pad operator simply adds \(\text{pad}_\text{in}\) at the start and \(\text{pad}_\text{end}\) at the end in forward mode:

\[y_{i} = x_{i-\text{pad}_\text{in}} \quad \forall i=\text{pad}_\text{in},\ldots,\text{pad}_\text{in}+N-1\]

and \(y_i = 0 \quad \forall i=0,\ldots,\text{pad}_\text{in}-1, \text{pad}_\text{in}+N-1,\ldots,N+\text{pad}_\text{in}+\text{pad}_\text{end}\)

In adjoint mode, values from \(\text{pad}_\text{in}\) to \(N-\text{pad}_\text{end}\) are extracted from the data:

\[x_{i} = y_{\text{pad}_\text{in}+i} \quad \forall i=0, N-1\]

Attributes

shapetuple

Operator shape

explicitbool

Operator contains a matrix that can be solved explicitly (True) or not (False)

Methods

__init__(dims, pad[, dtype, name])
adjoint()
apply_columns(cols)	Apply subset of columns of operator
cond([uselobpcg])	Condition number of linear operator.
conj()	Complex conjugate operator
div(y[, niter, densesolver])	Solve the linear problem \(\mathbf{y}=\mathbf{A}\mathbf{x}\).
dot(x)	Matrix-matrix or matrix-vector multiplication.
eigs([neigs, symmetric, niter, uselobpcg])	Most significant eigenvalues of linear operator.
matmat(X)	Matrix-matrix multiplication.
matvec(x)	Matrix-vector multiplication.
reset_count()	Reset counters
rmatmat(X)	Matrix-matrix multiplication.
rmatvec(x)	Adjoint matrix-vector multiplication.
todense([backend])	Return dense matrix.
toimag([forw, adj])	Imag operator
toreal([forw, adj])	Real operator
tosparse()	Return sparse matrix.
trace([neval, method, backend])	Trace of linear operator.
transpose()

Examples using pylops.Pad

Padding

Padding