MP, OMP, ISTA and FISTA

This example shows how to use the pylops.optimization.sparsity.omp, pylops.optimization.sparsity.irls, pylops.optimization.sparsity.ista, and pylops.optimization.sparsity.fista solvers.

These solvers can be used when the model to retrieve is supposed to have a sparse representation in a certain domain. MP and OMP use a L0 norm and mathematically translates to solving the following constrained problem:

\[\quad \|\mathbf{Op}\mathbf{x}- \mathbf{b}\|_2 <= \sigma,\]

while IRLS, ISTA and FISTA solve an uncostrained problem with a L1 regularization term:

\[J = \|\mathbf{d} - \mathbf{Op} \mathbf{x}\|_2 + \epsilon \|\mathbf{x}\|_1\]

import matplotlib.pyplot as plt
import numpy as np

import pylops

plt.close("all")
np.random.seed(0)

Let’s start with a simple example, where we create a dense mixing matrix and a sparse signal and we use OMP and ISTA to recover such a signal. Note that the mixing matrix leads to an underdetermined system of equations (\(N < M\)) so being able to add some extra prior information regarding the sparsity of our desired model is essential to be able to invert such a system.

N, M = 15, 20
A = np.random.randn(N, M)
A = A / np.linalg.norm(A, axis=0)
Aop = pylops.MatrixMult(A)

x = np.random.rand(M)
x[x < 0.9] = 0
y = Aop * x

# MP/OMP
eps = 1e-2
maxit = 500
x_mp = pylops.optimization.sparsity.omp(
    Aop, y, niter_outer=maxit, niter_inner=0, sigma=1e-4
)[0]
x_omp = pylops.optimization.sparsity.omp(Aop, y, niter_outer=maxit, sigma=1e-4)[0]

# IRLS
x_irls = pylops.optimization.sparsity.irls(
    Aop, y, nouter=50, epsI=1e-5, kind="model", **dict(iter_lim=10)
)[0]

# ISTA
x_ista = pylops.optimization.sparsity.ista(
    Aop,
    y,
    niter=maxit,
    eps=eps,
    tol=1e-3,
)[0]

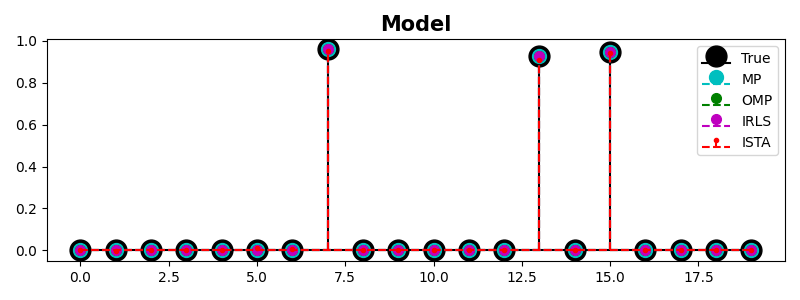
fig, ax = plt.subplots(1, 1, figsize=(8, 3))
m, s, b = ax.stem(x, linefmt="k", basefmt="k", markerfmt="ko", label="True")
plt.setp(m, markersize=15)
m, s, b = ax.stem(x_mp, linefmt="--c", basefmt="--c", markerfmt="co", label="MP")
plt.setp(m, markersize=10)
m, s, b = ax.stem(x_omp, linefmt="--g", basefmt="--g", markerfmt="go", label="OMP")
plt.setp(m, markersize=7)
m, s, b = ax.stem(x_irls, linefmt="--m", basefmt="--m", markerfmt="mo", label="IRLS")
plt.setp(m, markersize=7)
m, s, b = ax.stem(x_ista, linefmt="--r", basefmt="--r", markerfmt="ro", label="ISTA")
plt.setp(m, markersize=3)
ax.set_title("Model", size=15, fontweight="bold")
ax.legend()
plt.tight_layout()

We now consider a more interesting problem problem, wavelet deconvolution from a signal that we assume being composed by a train of spikes convolved with a certain wavelet. We will see how solving such a problem with a least-squares solver such as pylops.optimization.leastsquares.regularized_inversion does not produce the expected results (especially in the presence of noisy data), conversely using the pylops.optimization.sparsity.ista and pylops.optimization.sparsity.fista solvers allows us to succesfully retrieve the input signal even in the presence of noise. 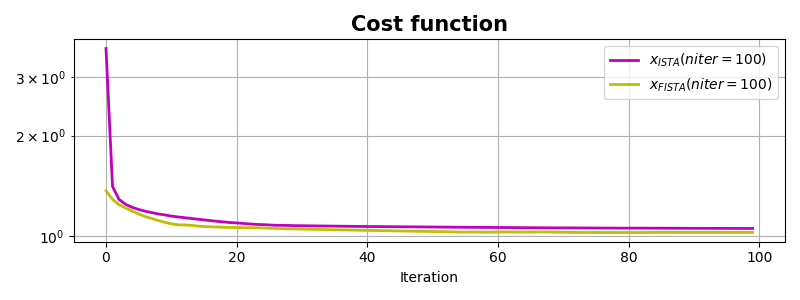pylops.optimization.sparsity.fista shows faster convergence which is particularly useful for this problem.

nt = 61
dt = 0.004
t = np.arange(nt) * dt
x = np.zeros(nt)
x[10] = -0.4
x[int(nt / 2)] = 1
x[nt - 20] = 0.5

h, th, hcenter = pylops.utils.wavelets.ricker(t[:21], f0=20)

Cop = pylops.signalprocessing.Convolve1D(nt, h=h, offset=hcenter, dtype="float32")
y = Cop * x
yn = y + np.random.normal(0, 0.1, y.shape)

# noise free
xls = Cop / y

xomp, nitero, costo = pylops.optimization.sparsity.omp(
    Cop, y, niter_outer=200, sigma=1e-8
)

xista, niteri, costi = pylops.optimization.sparsity.ista(
    Cop,
    y,
    niter=400,
    eps=5e-1,
    tol=1e-8,
)

fig, ax = plt.subplots(1, 1, figsize=(8, 3))
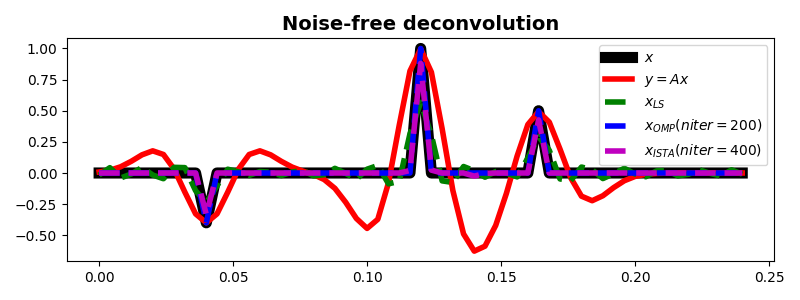
ax.plot(t, x, "k", lw=8, label=r"$x$")
ax.plot(t, y, "r", lw=4, label=r"$y=Ax$")
ax.plot(t, xls, "--g", lw=4, label=r"$x_{LS}$")
ax.plot(t, xomp, "--b", lw=4, label=r"$x_{OMP} (niter=%d)$" % nitero)
ax.plot(t, xista, "--m", lw=4, label=r"$x_{ISTA} (niter=%d)$" % niteri)
ax.set_title("Noise-free deconvolution", fontsize=14, fontweight="bold")
ax.legend()
plt.tight_layout()

# noisy
xls = pylops.optimization.leastsquares.regularized_inversion(
    Cop, yn, [], **dict(damp=1e-1, atol=1e-3, iter_lim=100, show=0)
)[0]

xista, niteri, costi = pylops.optimization.sparsity.ista(
    Cop,
    yn,
    niter=100,
    eps=5e-1,
    tol=1e-5,
)

xfista, niterf, costf = pylops.optimization.sparsity.fista(
    Cop,
    yn,
    niter=100,
    eps=5e-1,
    tol=1e-5,
)

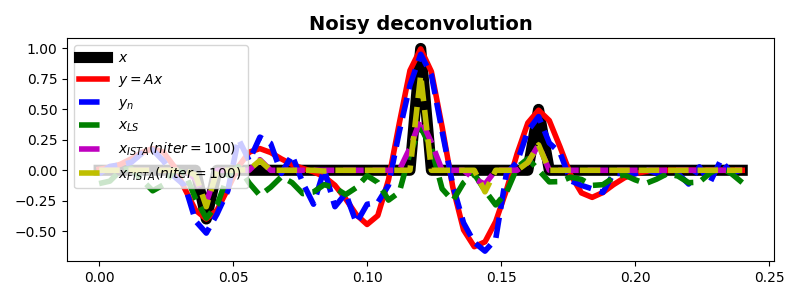
fig, ax = plt.subplots(1, 1, figsize=(8, 3))
ax.plot(t, x, "k", lw=8, label=r"$x$")
ax.plot(t, y, "r", lw=4, label=r"$y=Ax$")
ax.plot(t, yn, "--b", lw=4, label=r"$y_n$")
ax.plot(t, xls, "--g", lw=4, label=r"$x_{LS}$")
ax.plot(t, xista, "--m", lw=4, label=r"$x_{ISTA} (niter=%d)$" % niteri)
ax.plot(t, xfista, "--y", lw=4, label=r"$x_{FISTA} (niter=%d)$" % niterf)
ax.set_title("Noisy deconvolution", fontsize=14, fontweight="bold")
ax.legend()
plt.tight_layout()

fig, ax = plt.subplots(1, 1, figsize=(8, 3))
ax.semilogy(costi, "m", lw=2, label=r"$x_{ISTA} (niter=%d)$" % niteri)
ax.semilogy(costf, "y", lw=2, label=r"$x_{FISTA} (niter=%d)$" % niterf)
ax.set_title("Cost function", size=15, fontweight="bold")
ax.set_xlabel("Iteration")
ax.legend()
ax.grid(True, which="both")
plt.tight_layout()

• 
• 
•