pylops.signalprocessing.Radon2D#
- pylops.signalprocessing.Radon2D(taxis, haxis, pxaxis, kind='linear', centeredh=True, interp=True, onthefly=False, engine='numpy', dtype='float64', name='R')[source]#
Two dimensional Radon transform.
Apply two dimensional Radon forward (and adjoint) transform to a 2-dimensional array of size \([n_{p_x} \times n_t]\) (and \([n_x \times n_t]\)).
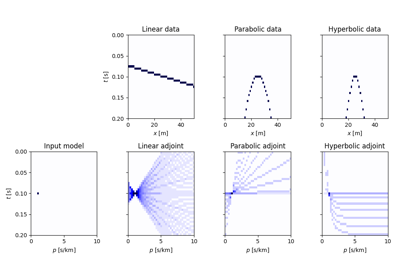
In forward mode this entails to spreading the model vector along parametric curves (lines, parabolas, or hyperbolas depending on the choice of
kind), while stacking values in the data vector along the same parametric curves is performed in adjoint mode.- Parameters
- taxis
np.ndarray Time axis
- haxis
np.ndarray Spatial axis
- pxaxis
np.ndarray Axis of scanning variable \(p_x\) of parametric curve
- kind
str, optional Curve to be used for stacking/spreading (
linear,parabolic, andhyperbolicare currently supported) or a function that takes \((x, t_0, p_x)\) as input and returns \(t\) as output- centeredh
bool, optional Assume centered spatial axis (
True) or not (False). IfTruethe originalhaxisis ignored and a new axis is created.- interp
bool, optional Apply linear interpolation (
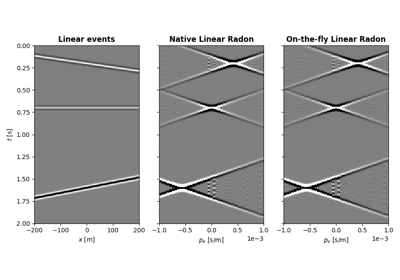
True) or nearest interpolation (False) during stacking/spreading along parametric curve- onthefly
bool, optional Compute stacking parametric curves on-the-fly as part of forward and adjoint modelling (
True) or at initialization and store them in look-up table (False). Using a look-up table is computationally more efficient but increases the memory burden- engine
str, optional Engine used for computation (
numpyornumba)- dtype
str, optional Type of elements in input array.
- name
str, optional New in version 2.0.0.
Name of operator (to be used by
pylops.utils.describe.describe)
- taxis
- Returns
- r2op
pylops.LinearOperator Radon operator
- r2op
- Raises
- KeyError
If
engineis neithernumpynornumba- NotImplementedError
If
kindis notlinear,parabolic, orhyperbolic
See also
pylops.signalprocessing.Radon3DThree dimensional Radon transform
pylops.SpreadSpread operator
Notes
The Radon2D operator applies the following linear transform in adjoint mode to the data after reshaping it into a 2-dimensional array of size \([n_x \times n_t]\) in adjoint mode:
\[m(p_x, t_0) = \int{d(x, t = f(p_x, x, t))} \,\mathrm{d}x\]where \(f(p_x, x, t) = t_0 + p_x x\) where \(p_x = \sin(\theta)/v\) in linear mode, \(f(p_x, x, t) = t_0 + p_x x^2\) in parabolic mode, and \(f(p_x, x, t) = \sqrt{t_0^2 + x^2 / p_x^2}\) in hyperbolic mode. Note that internally the \(p_x\) axis will be normalized by the ratio of the spatial and time axes and used alongside unitless axes. Whilst this makes the linear mode fully unitless, users are required to apply additional scalings to the \(p_x\) axis for other relationships:
\(p_x\) should be pre-multipled by \(d_x\) for the parabolic relationship;
\(p_x\) should be pre-multipled by \((d_t/d_x)^2\) for the hyperbolic relationship.
As the adjoint operator can be interpreted as a repeated summation of sets of elements of the model vector along chosen parametric curves, the forward is implemented as spreading of values in the data vector along the same parametric curves. This operator is actually a thin wrapper around the
pylops.Spreadoperator.