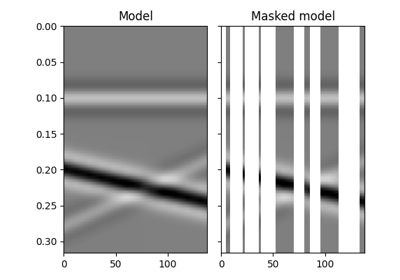
pylops.Spread#
- class pylops.Spread(dims, dimsd, table=None, dtable=None, fh=None, interp=None, engine='numpy', dtype='float64', name='S')[source]#
Spread operator.
Spread values from the input model vector arranged as a 2-dimensional array of size \([n_{x_0} \times n_{t_0}]\) into the data vector of size \([n_x \times n_t]\). Note that the value at each single pair \((x_0, t_0)\) in the input is spread over the entire \(x\) axis in the output.
Spreading is performed along parametric curves provided as look-up table of pre-computed indices (
table) or computed on-the-fly using a function handle (fh).In adjont mode, values from the data vector are instead stacked along the same parametric curves.
- Parameters
- dims
tuple Dimensions of model vector (vector will be reshaped internally into a two-dimensional array of size \([n_{x_0} \times n_{t_0}]\), where the first dimension is the spreading direction)
- dimsd
tuple Dimensions of data vector (vector will be reshaped internal into a two-dimensional array of size \([n_x \times n_t]\), where the first dimension is the stacking direction)
- table
np.ndarray, optional Look-up table of indices of size \([n_{x_0} \times n_{t_0} \times n_x]\) (if
Noneuse function handlefh). Whendtableis not provided, thedatawill be created as followsdata[ix, table[ix0, it0, ix]] += model[ix0, it0]
Note
When using
tablewithoutdtable, its elements must be between 0 and \(n_{t_0} - 1\) (ornumpy.nan).- dtable
np.ndarray, optional Look-up table of decimals remainders for linear interpolation of size \([n_{x_0} \times n_{t_0} \times n_x]\) (if
Noneuse function handlefh). When provided, thedatawill be created as followsdata[ix, table[ix0, it0, ix]] += (1 - dtable[ix0, it0, ix]) * model[ix0, it0] data[ix, table[ix0, it0, ix] + 1] += dtable[ix0, it0, ix] * model[ix0, it0]
Note
When using
tableanddtable, the elements oftableindices must be between 0 and \(n_{t_0} - 2\) (ornumpy.nan).- fh
callable, optional If
Nonewill use look-up tabletable. When provided, should be a function which takes indicesix0andit0and returns an array of size \(n_x\) containing each respective time index. Alternatively, if linear interpolation is required, it should output in addition to the time indices, a weight for interpolation with linear interpolation, to be used as followsdata[ix, index] += (1 - dindices[ix]) * model[ix0, it0] data[ix, index + 1] += dindices[ix] * model[ix0, it0]
where
indexrefers to a time index in the first array returned byfhanddindicesrefers to the weight in the second array returned byfh.Note
When using
fhwith one output (time indices), the time indices must be between 0 and \(n_{t_0} - 1\) (ornumpy.nan). When usingfhwith two outputs (time indices and weights), they must be within the between 0 and \(n_{t_0} - 2\) (ornumpy.nan).- interp
bool, optional Use only if engine
engine='numba'. Apply linear interpolation (True) or nearest interpolation (False) during stacking/spreading along parametric curve. When usingengine="numpy", it will be inferred directly fromfhor the presence ofdtable.- engine
str, optional Engine used for spread computation (
numpyornumba). Note thatnumbacan only be used when providing a look-up table- dtype
str, optional Type of elements in input array.
- name
str, optional New in version 2.0.0.
Name of operator (to be used by
pylops.utils.describe.describe)
- dims
- Raises
- KeyError
If
engineis neithernumpynornumba- NotImplementedError
If both
tableandfhare not provided- ValueError
If
tablehas shape different from \([n_{x_0} \times n_{t_0} \times n_x]\)
Notes
The Spread operator applies the following linear transform in forward mode to the model vector after reshaping it into a 2-dimensional array of size \([n_x \times n_t]\):
\[m(x_0, t_0) \rightarrow d(x, t=f(x_0, x, t_0)) \quad \forall x\]where \(f(x_0, x, t)\) is a mapping function that returns a value \(t\) given values \(x_0\), \(x\), and \(t_0\). Note that for each \((x_0, t_0)\) pair, spreading is done over the entire \(x\) axis in the data domain.
In adjoint mode, the model is reconstructed by means of the following stacking operation:
\[m(x_0, t_0) = \int{d(x, t=f(x_0, x, t_0))} \,\mathrm{d}x\]Note that
table(orfh) must return integer numbers representing indices in the axis \(t\). However it also possible to perform linear interpolation as part of the spreading/stacking process by providing the decimal part of the mapping function (\(t - \lfloor t \rfloor\)) either indtableinput parameter or as second value in the return offhfunction.- Attributes
Methods
__init__(dims, dimsd[, table, dtable, fh, ...])adjoint()apply_columns(cols)Apply subset of columns of operator
cond([uselobpcg])Condition number of linear operator.
conj()Complex conjugate operator
div(y[, niter, densesolver])Solve the linear problem \(\mathbf{y}=\mathbf{A}\mathbf{x}\).
dot(x)Matrix-matrix or matrix-vector multiplication.
eigs([neigs, symmetric, niter, uselobpcg])Most significant eigenvalues of linear operator.
matmat(X)Matrix-matrix multiplication.
matvec(x)Matrix-vector multiplication.
reset_count()Reset counters
rmatmat(X)Matrix-matrix multiplication.
rmatvec(x)Adjoint matrix-vector multiplication.
todense([backend])Return dense matrix.
toimag([forw, adj])Imag operator
toreal([forw, adj])Real operator
tosparse()Return sparse matrix.
trace([neval, method, backend])Trace of linear operator.
transpose()