Note
Go to the end to download the full example code
Shift#
This example shows how to use the pylops.signalprocessing.Shift
operator to apply fractional delay to an input signal. Whilst this operator
acts on 1D signals it can also be applied on any multi-dimensional signal on
a specific direction of it.
import matplotlib.pyplot as plt
import numpy as np
import pylops
plt.close("all")
Let’s start with a 1D example. Define the input parameters: number of samples
of input signal (nt), sampling step (dt) as well as the input
signal which will be equal to a ricker wavelet:
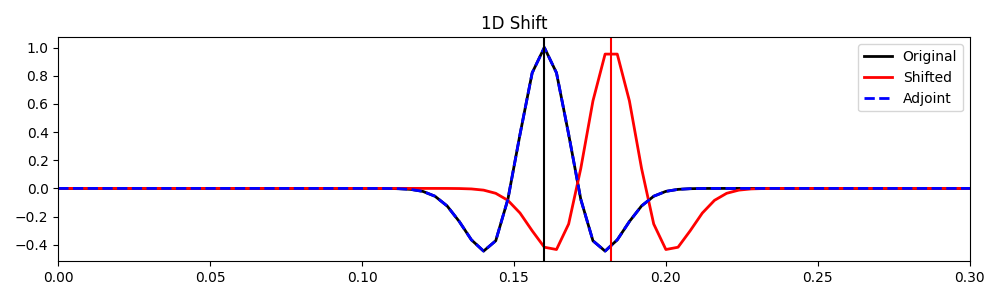
We can shift this wavelet by \(5.5\mathrm{dt}\):
shift = 5.5 * dt
Op = pylops.signalprocessing.Shift(nt, shift, sampling=dt, real=True, dtype=np.float64)
wavshift = Op * wav
wavshiftback = Op.H * wavshift
plt.figure(figsize=(10, 3))
plt.plot(t, wav, "k", lw=2, label="Original")
plt.plot(t, wavshift, "r", lw=2, label="Shifted")
plt.plot(t, wavshiftback, "--b", lw=2, label="Adjoint")
plt.axvline(t[ntwav - 1], color="k")
plt.axvline(t[ntwav - 1] + shift, color="r")
plt.xlim(0, 0.3)
plt.legend()
plt.title("1D Shift")
plt.tight_layout()
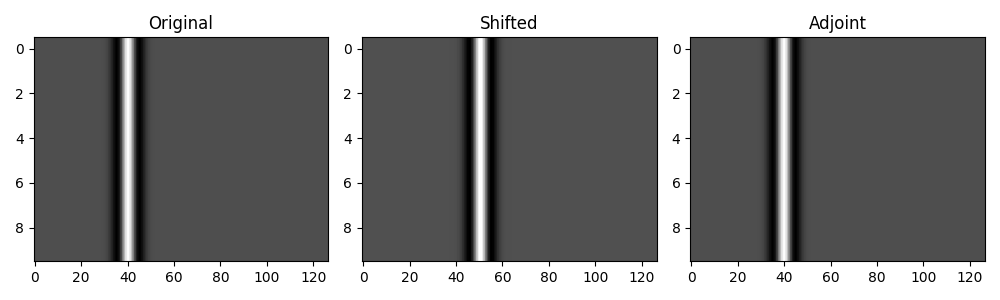
We can repeat the same exercise for a 2D signal and perform the shift along the first and second dimensions.
shift = 10.5 * dt
# 1st axis
wav2d = np.outer(wav, np.ones(10))
Op = pylops.signalprocessing.Shift(
(nt, 10), shift, axis=0, sampling=dt, real=True, dtype=np.float64
)
wav2dshift = Op * wav2d
wav2dshiftback = Op.H * wav2dshift
fig, axs = plt.subplots(1, 3, figsize=(10, 3))
axs[0].imshow(wav2d, cmap="gray")
axs[0].axis("tight")
axs[0].set_title("Original")
axs[1].imshow(wav2dshift, cmap="gray")
axs[1].set_title("Shifted")
axs[1].axis("tight")
axs[2].imshow(wav2dshiftback, cmap="gray")
axs[2].set_title("Adjoint")
axs[2].axis("tight")
fig.tight_layout()
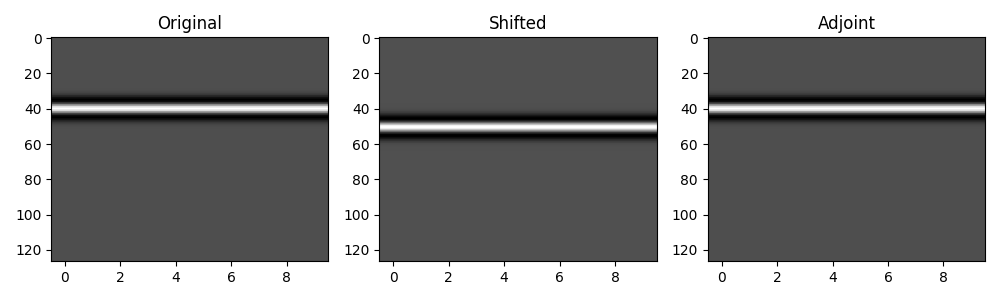
# 2nd axis
wav2d = np.outer(wav, np.ones(10)).T
Op = pylops.signalprocessing.Shift(
(10, nt), shift, axis=1, sampling=dt, real=True, dtype=np.float64
)
wav2dshift = Op * wav2d
wav2dshiftback = Op.H * wav2dshift
fig, axs = plt.subplots(1, 3, figsize=(10, 3))
axs[0].imshow(wav2d, cmap="gray")
axs[0].axis("tight")
axs[0].set_title("Original")
axs[1].imshow(wav2dshift, cmap="gray")
axs[1].set_title("Shifted")
axs[1].axis("tight")
axs[2].imshow(wav2dshiftback, cmap="gray")
axs[2].set_title("Adjoint")
axs[2].axis("tight")
fig.tight_layout()
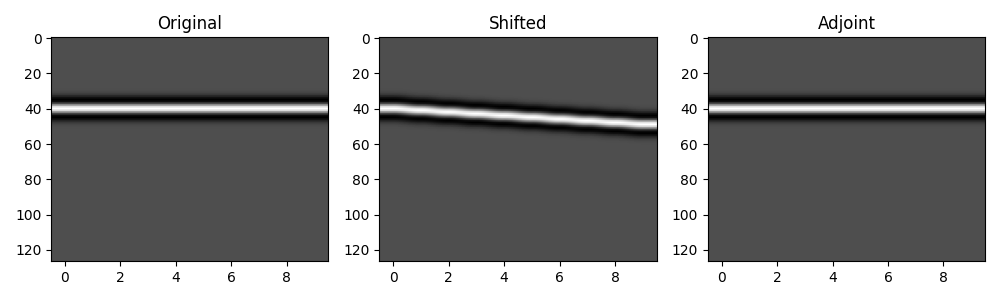
Finally we consider a more generic case where we apply a trace varying shift
shift = dt * np.arange(10)
wav2d = np.outer(wav, np.ones(10))
Op = pylops.signalprocessing.Shift(
(nt, 10), shift, axis=0, sampling=dt, real=True, dtype=np.float64
)
wav2dshift = Op * wav2d
wav2dshiftback = Op.H * wav2dshift
fig, axs = plt.subplots(1, 3, figsize=(10, 3))
axs[0].imshow(wav2d, cmap="gray")
axs[0].axis("tight")
axs[0].set_title("Original")
axs[1].imshow(wav2dshift, cmap="gray")
axs[1].set_title("Shifted")
axs[1].axis("tight")
axs[2].imshow(wav2dshiftback, cmap="gray")
axs[2].set_title("Adjoint")
axs[2].axis("tight")
fig.tight_layout()
Total running time of the script: (0 minutes 1.502 seconds)