Note
Go to the end to download the full example code
Derivatives#
This example shows how to use the suite of derivative operators, namely
pylops.FirstDerivative, pylops.SecondDerivative,
pylops.Laplacian and pylops.Gradient,
pylops.FirstDirectionalDerivative and
pylops.SecondDirectionalDerivative.
The derivative operators are very useful when the model to be inverted for is expect to be smooth in one or more directions. As shown in the Optimization tutorial, these operators will be used as part of the regularization term to obtain a smooth solution.
import matplotlib.pyplot as plt
import numpy as np
import pylops
plt.close("all")
np.random.seed(0)
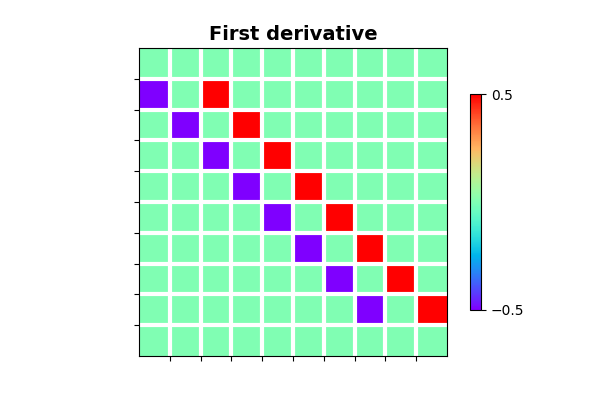
Let’s start by looking at a simple first-order centered derivative and how could implement it naively by creating a dense matrix. Note that we will not apply the derivative where the stencil is partially outside of the range of the input signal (i.e., at the edge of the signal)
nx = 10
D = np.diag(0.5 * np.ones(nx - 1), k=1) - np.diag(0.5 * np.ones(nx - 1), -1)
D[0] = D[-1] = 0
fig, ax = plt.subplots(1, 1, figsize=(6, 4))
im = plt.imshow(D, cmap="rainbow", vmin=-0.5, vmax=0.5)
ax.set_title("First derivative", size=14, fontweight="bold")
ax.set_xticks(np.arange(nx - 1) + 0.5)
ax.set_yticks(np.arange(nx - 1) + 0.5)
ax.grid(linewidth=3, color="white")
ax.xaxis.set_ticklabels([])
ax.yaxis.set_ticklabels([])
fig.colorbar(im, ax=ax, ticks=[-0.5, 0.5], shrink=0.7)
<matplotlib.colorbar.Colorbar object at 0x7f2f741ffb50>
We now create a signal filled with zero and a single one at its center and apply the derivative matrix by means of a dot product
Let’s now do the same using the pylops.FirstDerivative operator
and compare its outputs after applying the forward and adjoint operators
to those from the dense matrix.
D1op = pylops.FirstDerivative(nx, dtype="float32")
y_lop = D1op * x
xadj_lop = D1op.H * y_lop
fig, axs = plt.subplots(3, 1, figsize=(13, 8), sharex=True)
axs[0].stem(np.arange(nx), x, linefmt="k", markerfmt="ko")
axs[0].set_title("Input", size=20, fontweight="bold")
axs[1].stem(np.arange(nx), y_dir, linefmt="k", markerfmt="ko", label="direct")
axs[1].stem(np.arange(nx), y_lop, linefmt="--r", markerfmt="ro", label="lop")
axs[1].set_title("Forward", size=20, fontweight="bold")
axs[1].legend()
axs[2].stem(np.arange(nx), xadj_dir, linefmt="k", markerfmt="ko", label="direct")
axs[2].stem(np.arange(nx), xadj_lop, linefmt="--r", markerfmt="ro", label="lop")
axs[2].set_title("Adjoint", size=20, fontweight="bold")
axs[2].legend()
plt.tight_layout()
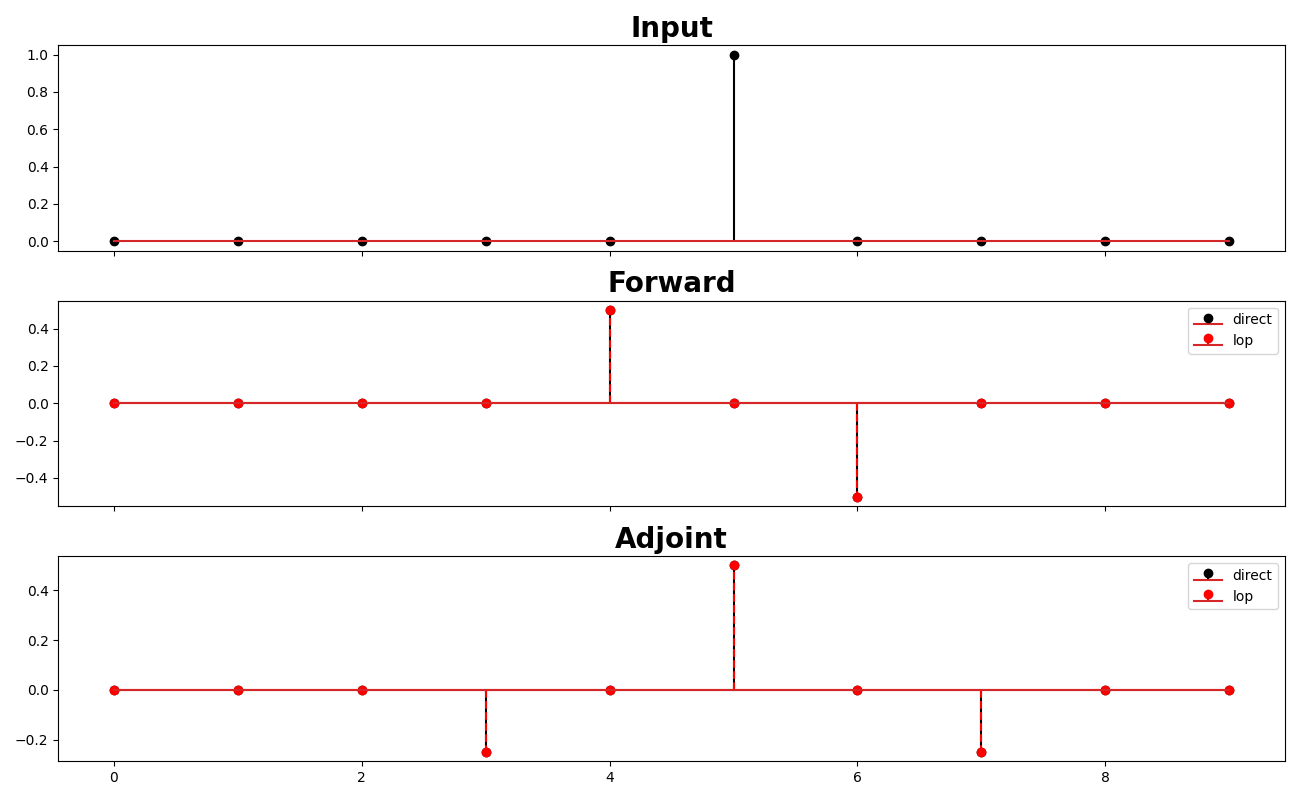
As expected we obtain the same result, with the only difference that in the second case we did not need to explicitly create a matrix, saving memory and computational time.
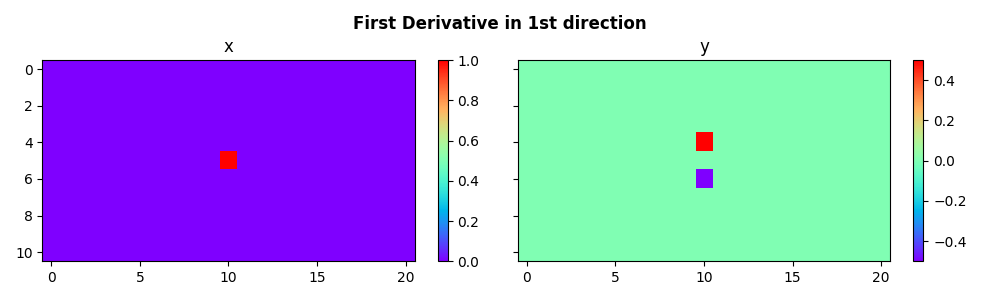
Let’s move onto applying the same first derivative to a 2d array in the first direction
nx, ny = 11, 21
A = np.zeros((nx, ny))
A[nx // 2, ny // 2] = 1.0
D1op = pylops.FirstDerivative((nx, ny), axis=0, dtype="float64")
B = D1op * A
fig, axs = plt.subplots(1, 2, figsize=(10, 3), sharey=True)
fig.suptitle(
"First Derivative in 1st direction", fontsize=12, fontweight="bold", y=0.95
)
im = axs[0].imshow(A, interpolation="nearest", cmap="rainbow")
axs[0].axis("tight")
axs[0].set_title("x")
plt.colorbar(im, ax=axs[0])
im = axs[1].imshow(B, interpolation="nearest", cmap="rainbow")
axs[1].axis("tight")
axs[1].set_title("y")
plt.colorbar(im, ax=axs[1])
plt.tight_layout()
plt.subplots_adjust(top=0.8)
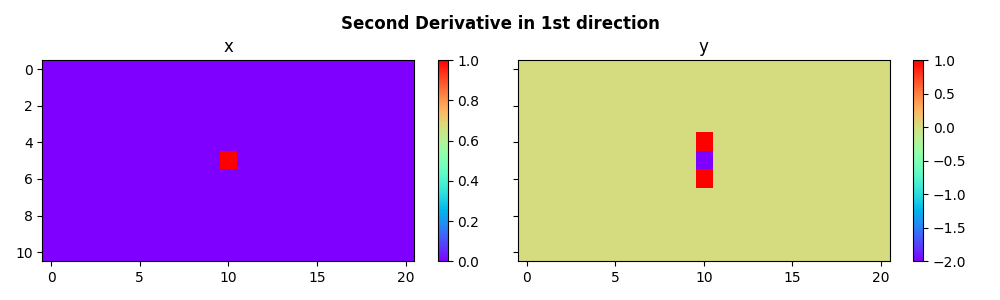
We can now do the same for the second derivative
A = np.zeros((nx, ny))
A[nx // 2, ny // 2] = 1.0
D2op = pylops.SecondDerivative(dims=(nx, ny), axis=0, dtype="float64")
B = D2op * A
fig, axs = plt.subplots(1, 2, figsize=(10, 3), sharey=True)
fig.suptitle(
"Second Derivative in 1st direction", fontsize=12, fontweight="bold", y=0.95
)
im = axs[0].imshow(A, interpolation="nearest", cmap="rainbow")
axs[0].axis("tight")
axs[0].set_title("x")
plt.colorbar(im, ax=axs[0])
im = axs[1].imshow(B, interpolation="nearest", cmap="rainbow")
axs[1].axis("tight")
axs[1].set_title("y")
plt.colorbar(im, ax=axs[1])
plt.tight_layout()
plt.subplots_adjust(top=0.8)
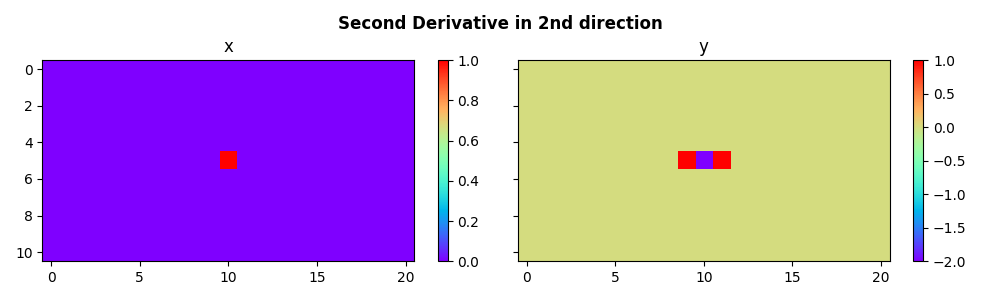
We can also apply the second derivative to the second direction of
our data (axis=1)
D2op = pylops.SecondDerivative(dims=(nx, ny), axis=1, dtype="float64")
B = D2op * A
fig, axs = plt.subplots(1, 2, figsize=(10, 3), sharey=True)
fig.suptitle(
"Second Derivative in 2nd direction", fontsize=12, fontweight="bold", y=0.95
)
im = axs[0].imshow(A, interpolation="nearest", cmap="rainbow")
axs[0].axis("tight")
axs[0].set_title("x")
plt.colorbar(im, ax=axs[0])
im = axs[1].imshow(B, interpolation="nearest", cmap="rainbow")
axs[1].axis("tight")
axs[1].set_title("y")
plt.colorbar(im, ax=axs[1])
plt.tight_layout()
plt.subplots_adjust(top=0.8)
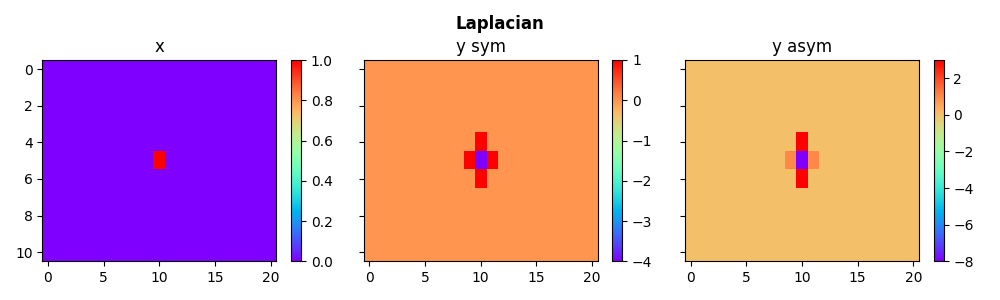
We use the symmetrical Laplacian operator as well as a asymmetrical version of it (by adding more weight to the derivative along one direction)
# symmetrical
L2symop = pylops.Laplacian(dims=(nx, ny), weights=(1, 1), dtype="float64")
# asymmetrical
L2asymop = pylops.Laplacian(dims=(nx, ny), weights=(3, 1), dtype="float64")
Bsym = L2symop * A
Basym = L2asymop * A
fig, axs = plt.subplots(1, 3, figsize=(10, 3), sharey=True)
fig.suptitle("Laplacian", fontsize=12, fontweight="bold", y=0.95)
im = axs[0].imshow(A, interpolation="nearest", cmap="rainbow")
axs[0].axis("tight")
axs[0].set_title("x")
plt.colorbar(im, ax=axs[0])
im = axs[1].imshow(Bsym, interpolation="nearest", cmap="rainbow")
axs[1].axis("tight")
axs[1].set_title("y sym")
plt.colorbar(im, ax=axs[1])
im = axs[2].imshow(Basym, interpolation="nearest", cmap="rainbow")
axs[2].axis("tight")
axs[2].set_title("y asym")
plt.colorbar(im, ax=axs[2])
plt.tight_layout()
plt.subplots_adjust(top=0.8)
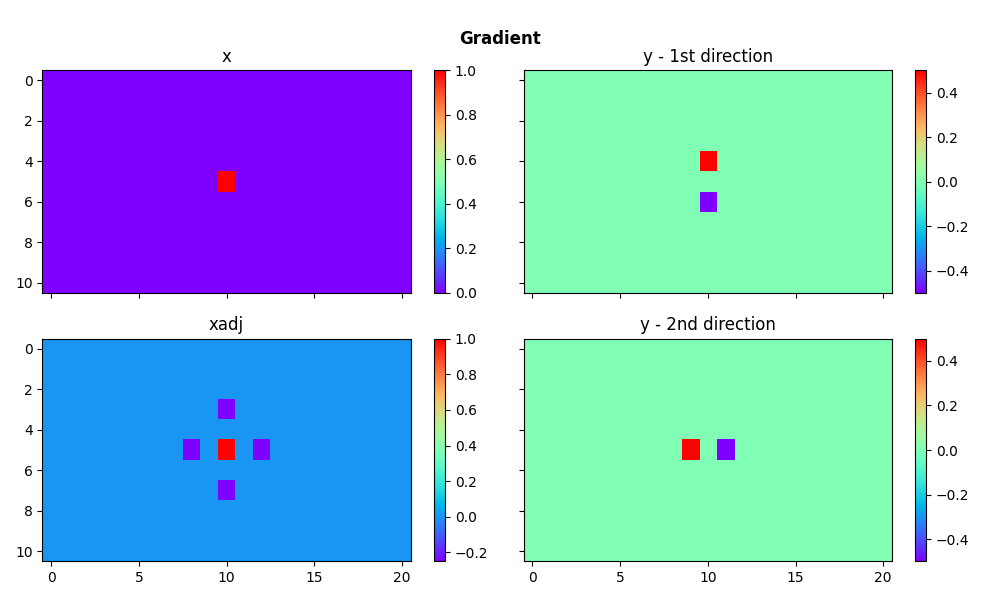
We consider now the gradient operator. Given a 2-dimensional array, this operator applies first-order derivatives on both dimensions and concatenates them.
Gop = pylops.Gradient(dims=(nx, ny), dtype="float64")
B = Gop * A
C = Gop.H * B
fig, axs = plt.subplots(2, 2, figsize=(10, 6), sharex=True, sharey=True)
fig.suptitle("Gradient", fontsize=12, fontweight="bold", y=0.95)
im = axs[0, 0].imshow(A, interpolation="nearest", cmap="rainbow")
axs[0, 0].axis("tight")
axs[0, 0].set_title("x")
plt.colorbar(im, ax=axs[0, 0])
im = axs[0, 1].imshow(B[0, ...], interpolation="nearest", cmap="rainbow")
axs[0, 1].axis("tight")
axs[0, 1].set_title("y - 1st direction")
plt.colorbar(im, ax=axs[0, 1])
im = axs[1, 1].imshow(B[1, ...], interpolation="nearest", cmap="rainbow")
axs[1, 1].axis("tight")
axs[1, 1].set_title("y - 2nd direction")
plt.colorbar(im, ax=axs[1, 1])
im = axs[1, 0].imshow(C, interpolation="nearest", cmap="rainbow")
axs[1, 0].axis("tight")
axs[1, 0].set_title("xadj")
plt.colorbar(im, ax=axs[1, 0])
plt.tight_layout()
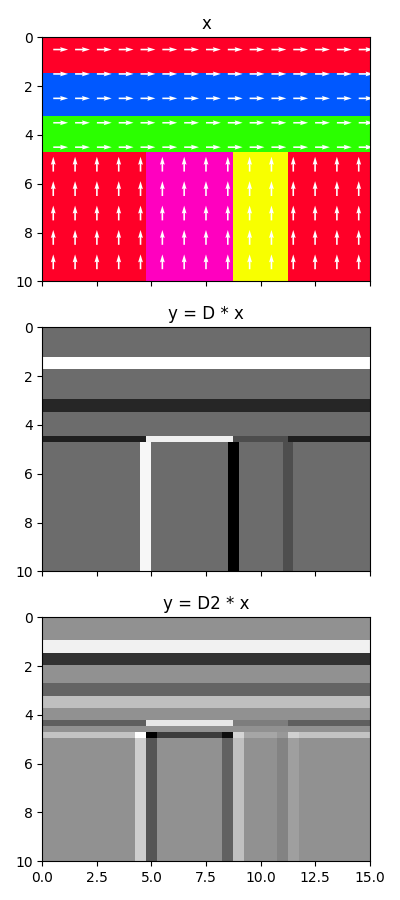
Finally we use the Gradient operator to compute directional derivatives. We create a model which has some layering in the horizontal and vertical directions and show how the direction derivatives differs from standard derivatives
nx, nz = 60, 40
horlayers = np.cumsum(np.random.uniform(2, 10, 20).astype(int))
horlayers = horlayers[horlayers < nz // 2]
nhorlayers = len(horlayers)
vertlayers = np.cumsum(np.random.uniform(2, 20, 10).astype(int))
vertlayers = vertlayers[vertlayers < nx]
nvertlayers = len(vertlayers)
A = 1500 * np.ones((nz, nx))
for top, base in zip(horlayers[:-1], horlayers[1:]):
A[top:base] = np.random.normal(2000, 200)
for top, base in zip(vertlayers[:-1], vertlayers[1:]):
A[horlayers[-1] :, top:base] = np.random.normal(2000, 200)
v = np.zeros((2, nz, nx))
v[0, : horlayers[-1]] = 1
v[1, horlayers[-1] :] = 1
Ddop = pylops.FirstDirectionalDerivative((nz, nx), v=v, sampling=(nz, nx))
D2dop = pylops.SecondDirectionalDerivative((nz, nx), v=v, sampling=(nz, nx))
dirder = Ddop * A
dir2der = D2dop * A
jump = 4
fig, axs = plt.subplots(3, 1, figsize=(4, 9), sharex=True)
im = axs[0].imshow(A, cmap="gist_rainbow", extent=(0, nx // jump, nz // jump, 0))
q = axs[0].quiver(
np.arange(nx // jump) + 0.5,
np.arange(nz // jump) + 0.5,
np.flipud(v[1, ::jump, ::jump]),
np.flipud(v[0, ::jump, ::jump]),
color="w",
linewidths=20,
)
axs[0].set_title("x")
axs[0].axis("tight")
axs[1].imshow(dirder, cmap="gray", extent=(0, nx // jump, nz // jump, 0))
axs[1].set_title("y = D * x")
axs[1].axis("tight")
axs[2].imshow(dir2der, cmap="gray", extent=(0, nx // jump, nz // jump, 0))
axs[2].set_title("y = D2 * x")
axs[2].axis("tight")
plt.tight_layout()
Total running time of the script: (0 minutes 3.695 seconds)
