pylops.signalprocessing.Sliding2D#
- pylops.signalprocessing.Sliding2D(Op, dims, dimsd, nwin, nover, tapertype='hanning', name='S')[source]#
2D Sliding transform operator.
Apply a transform operator
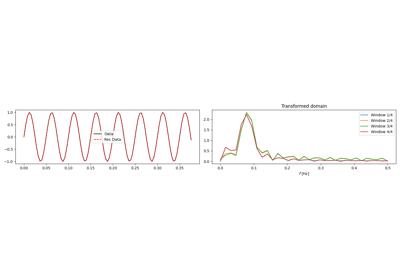
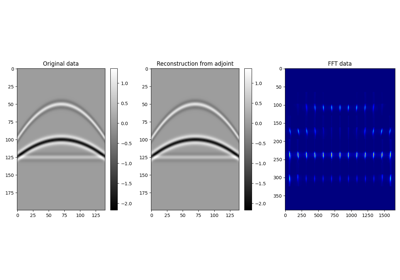
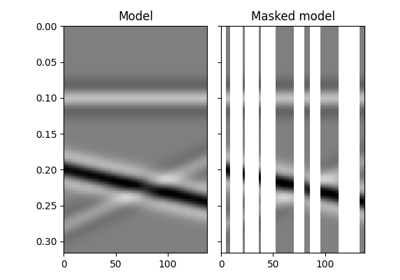
Oprepeatedly to slices of the model vector in forward mode and slices of the data vector in adjoint mode. More specifically, in forward mode the model vector is divided into slices, each slice is transformed, and slices are then recombined in a sliding window fashion. Both model and data are internally reshaped and interpreted as 2-dimensional arrays: each slice contains a portion of the array in the first dimension (and the entire second dimension).This operator can be used to perform local, overlapping transforms (e.g.,
pylops.signalprocessing.FFT2Dorpylops.signalprocessing.Radon2D) on 2-dimensional arrays.Note
The shape of the model has to be consistent with the number of windows for this operator not to return an error. As the number of windows depends directly on the choice of
nwinandnover, it is recommended to first runsliding2d_designto obtain the correspondingdimsand number of windows.Warning
Depending on the choice of nwin and nover as well as the size of the data, sliding windows may not cover the entire data. The start and end indices of each window will be displayed and returned with running
sliding2d_design.- Parameters
- Op
pylops.LinearOperator Transform operator
- dims
tuple Shape of 2-dimensional model. Note that
dims[0]should be multiple of the model size of the transform in the first dimension- dimsd
tuple Shape of 2-dimensional data
- nwin
int Number of samples of window
- nover
int Number of samples of overlapping part of window
- tapertype
str, optional Type of taper (
hanning,cosine,cosinesquareorNone)- name
str, optional New in version 2.0.0.
Name of operator (to be used by
pylops.utils.describe.describe)
- Op
- Returns
- Sop
pylops.LinearOperator Sliding operator
- Sop
- Raises
- ValueError
Identified number of windows is not consistent with provided model shape (
dims).